Моменты инерции некоторых однородных тел

Лабораторная работа №1

Определение момента инерции различных тел.

Теорема Штейнера.

Цель работы: определение момента инерции различных тел, проверка справедливости теоремы Гюйгенса–Штейнера.

Оборудование
Вращающийся вал Диск с диаметральными отверстиями Динамометр, 2 Н Световой барьер со счетчиком Источник питания, 5 В/2,4 А Треножник «PASS» Цилиндрическая опора «PASS» Линейка, пластмассовая,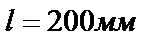

Ключевые слова

Твердое тело, момент инерции, центр тяжести, ось вращения, крутильное колебание, жесткость пружины, возвращающая сила.

ТЕОРИЯ

Поступательное и вращательное движения являются частными проявлениями общего процесса механического движения материи. Физическое единство отражается в аналогии математической формы записи законов, описывающих эти виды движения. Основной закон динамики поступательного движения описывается выражением

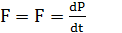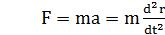или (1)

Величина m – масса тела – выражает численно меру инертности тела, т.е. его способность изменять состояние поступательного движения под действием силы F. Основной закон динамики вращательного движения твердого тела, вращающегося вокруг оси симметрии тела, записывается в виде

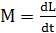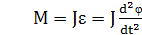или (1а)

где

L- момент импульса тела;

j - вектор углового перемещения;

e- угловое ускорение;

M- момент силы.

Коэффициент пропорциональности J носит название момента инерции. Момент инерции является мерой инерции тела во вращательном движении и определяет способность тела изменять состояние вращательного движения под действием момента силы M. Размерность момента инерции в системе СИ – [кг×м²]. Исходя из размерности момента инерции, можно дать определение момента инерции материальной точки относительно оси вращения в виде

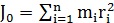(2)

где

r_i – радиус вращения материальной точки,

m_i – ее масса.

Масса реального тела представляется в виде суммы масс материальных точек, его составляющих. Аналогично этому, момент инерции тела есть совокупность моментов инерции его частей, рассматриваемых как материальные точки:

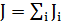(3)

Для тел правильной геометрической формы суммирование (а в пределе – интегрирование) по (3) дает следующие результаты для моментов инерции, вычисленных относительно оси, проходящей через центр симметрии этих тел:

Моменты инерции некоторых однородных тел

Диск или цилиндр вращающийся вокруг центральной оси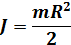
Момент инерции стержня при вращении относительно оси, проходящей через его конец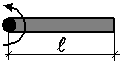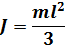
Момент инерции стержня при вращении относительно оси, проходящей через его центр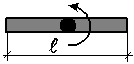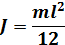
Момент инерции шара при вращении относительно оси, проходящей через его центр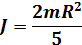

где

r – радиус соответствующих тел,

m – их масса.

m

C

О

А

А

l

О

Рис. 1

Если необходимо рассчитать момент инерции тела относительно оси А, не проходящей через центр симметрии, но параллельной ей (рис. 1), можно воспользоваться теоремой Гюйгенса–Штейнера: «Момент инерции тела J_А относительно любой оси А параллельной оси О, проходящей через центр симметрии тела, равен моменту инерции J_о этого тела относительно оси О, сложенному с величиной m l²; l=r- расстояние между осями А и О; m – масса тела

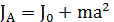(4)

Используя формулы (3) и (4), можно аналитически рассчитать момент инерции любого тела, условно разделяя его на составные части правильной геометрической формы и определяя расстояния, на которых они находятся от общей оси вращения тела. В случаях, когда аналитическое определение момента инерции затруднено сложностью формы тела или неоднородностью распределения массы, его определяют опытным путем, что является одной из целей настоящей работы.