Непрерывную кривую, которую описывает точка в своем движении, называют траекторией точки. Если траектория точки является прямой линией, то движение точки называют прямолинейным. Если же траектория – кривая линия (не обязательно плоская), то движение точки называется криволинейным.
Движение точки по отношению к выбранной системе координат считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени.
В теоретической механике используются три основных способа задания движения точки: векторный, координатный и естественный.
При векторном способе положение точки в пространстве определяется радиус-вектором 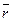 , проводимым из какого-либо заданного центра
, проводимым из какого-либо заданного центра
(рис. 2.1). Таким образом, траектория движения точки является геометрическим местом концов радиус-вектора 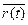 движущейся точки. Равенство
движущейся точки. Равенство 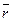 =
= 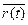 называют законом или уравнением движения точки в векторной форме.
называют законом или уравнением движения точки в векторной форме.
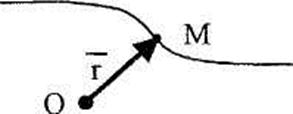
Рис. 2.1
Векторный способ задания движения используется в основном при теоретических выкладках, так как он значительно упрощает многие выводы и иногда подчеркивает физическую сущность явлений. Следует, однако, иметь в виду, что задать вектор как функцию времени, значит уметь находить его модуль и направление в любой момент времени. Это можно сделать, если избрана какая-либо определенная система координат. При решении конкретных задач обычно переходят от векторного к координатному и естественному способам задания движения.
При координатном способе положение точки определяется координатами точки в выбранной системе координат. Наиболее часто используется прямоугольная декартова система координат Oxyz (рис. 2.2). При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты x,y,z движущейся точки М являются функциями времени, то есть:
x = x(t), y = y(t), z = z(t).
Эти равенства называются законом или уравнениями движения точки в декартовых координатах.
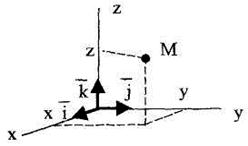
Рис. 2.2
Естественный способ задания положения и движения точки применяется в тех случаях, когда траектория движения точки заранее известна. На траектории выбирается некоторая неподвижная (относительно траектории) точка О, которая называется началом отсчета дуговой координаты (рис. 2.3). Положение движущейся точки М на траектории определяется дуговой координатой, то есть расстоянием OM=s, отложенным по траектории от начала отсчета О.
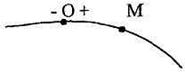
Рис. 2.3
Расстояния, отложенные в одну сторону от точки О, считают положительными, а в противоположную – отрицательными. То есть, устанавливается направление отсчета дуговой координаты.
При движении точки М расстояние s от этой точки до «неподвижной» точки О изменяется с течением времени, то есть дуговая координата s является функцией времени s=s(t). Эта равенство называется законом или уравнением движения точки в естественной форме.
Скорость — это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета (рис. 2.4). Направление вектора характеризует направление движения точки, модуль вектора – быстроту движения. Принято вектор скорости обозначать буквой 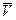 . Очень важно помнить, что вектор скорости всегда направлен по касательной к траектории движения в данной точке.
. Очень важно помнить, что вектор скорости всегда направлен по касательной к траектории движения в данной точке.

Рис. 2.4
Размерность скорости равна единице измерения длины, деленной на единицу измерения времени. Единицы измерения могут быть м/с, см/с, км/ч и т.д. В системе СИ единица измерения скорости м/с.
При векторном способе задания движения точки скорость определяется как первая производная от радиус-вектора по времени:
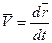 (2.1)
(2.1)
При координатном способе задания движения точки ее скорость определяется как вектор:
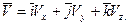 (2.2)
(2.2)
где 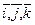 – единичные векторы (орты), определяющие направление осей координат, Vx,Vy,Vz – проекции вектора скорости на координатные оси, причем
– единичные векторы (орты), определяющие направление осей координат, Vx,Vy,Vz – проекции вектора скорости на координатные оси, причем
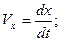
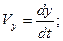
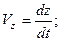 (2.3)
(2.3)
где x,y,z – координаты точки М.
To есть проекции вектора скорости на координатные оси равны первым производным по времени от соответствующих координат точки. Модуль скорости определяется формулой
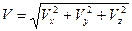 (2.4)
(2.4)
направляющими косинусами:
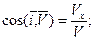
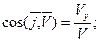
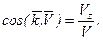 (2.5)
(2.5)
При естественном способе задания движения скорость определяется формулой
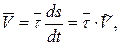 (2.6)
(2.6)
где 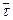 – единичный вектор касательной к траектории в данной точке
– единичный вектор касательной к траектории в данной точке
(рис. 2.5), направленный в сторону положительного отсчета дуговой координаты s, 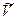 – алгебраическое значение скорости:
– алгебраическое значение скорости:
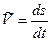 (2.7)
(2.7)
От модуля скорости V алгебраическая величина отличается наличием знака + или -. Если 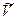 > О, то вектор
> О, то вектор 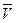 направлен в сторону положительного отсчета дуговой координаты (
направлен в сторону положительного отсчета дуговой координаты (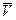
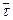 ); если
); если 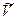 <0, то в отрицательную (
<0, то в отрицательную (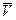 ¯
¯ 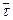 ). Заметим, что
). Заметим, что
| 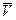 | = |
| = | 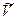 |.
|.
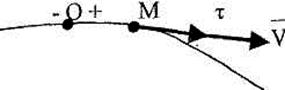
Рис. 2.5
При неравномерном движении точки по траектории изменяются модуль и направление скорости. Ускорением точки называется векторная величина, характеризующая быстроту изменения модуля и направления скорости. В литературе принято вектор ускорения обозначать 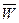 или
или 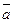 . Про направление вектора ускорения относительно траектории движения точки достоверно можно сказать только то, что он всегда направлен в сторону вогнутости кривой траектории движения (рис. 2.6).
. Про направление вектора ускорения относительно траектории движения точки достоверно можно сказать только то, что он всегда направлен в сторону вогнутости кривой траектории движения (рис. 2.6).
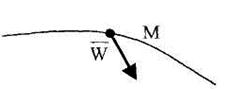
Рис. 2.6
Размерность ускорения равна единицам измерения длины, деленным на единицу измерения времени в квадрате. Единицы измерения могут быть м/с2, см/с2 и т.д. В системе СИ единица измерения ускорения м/с2.
При векторном способе задания движения ускорение точки определяется как первая производная от вектора скорости или вторая производная от радиус-вектора по времени:
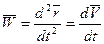 (2.8)
(2.8)
При координатном способе задания движения ускорение точки определяется как вектор:
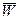 =
= 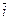 Wx +
Wx + 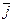 Wy+
Wy+ 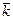 Wz, (2.9)
Wz, (2.9)
где Wx,Wy,Wz – проекции вектора ускорения на координатные оси, причем
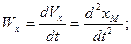
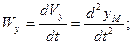
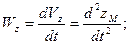 (2.10)
(2.10)
To есть проекции вектора ускорения на координатные оси равны первым производным по времени от соответствующих проекций вектора скорости или вторым производным по времени от координат точки.
Модуль вектора ускорения в этом случае определяется формулой
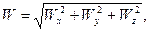 (2.11)
(2.11)
а направление в пространстве – направляющими косинусами:
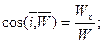
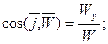
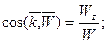 (2.12)
(2.12)
При естественном способе задания движения точки вектор ускорения складывается из двух взаимно перпендикулярных составляющих – нормальной 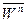 и касательной
и касательной 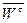 . Для определения направлений этих составляющих рассмотрим пространственную кривую (рис. 2.7).
. Для определения направлений этих составляющих рассмотрим пространственную кривую (рис. 2.7).
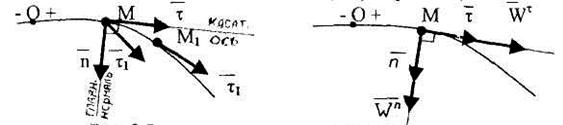
Рис. 2.7 Рис. 2.8
Проведем в некоторой произвольной точке М этой кривой касательную. Ось, проводимая из точки М по касательной в сторону положительного приращения дуговой координаты s=OM, называется касательной осью. Ее направление принято характеризовать единичным вектором (ортом) 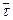 . Пусть
. Пусть 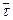 1 – единичный вектор, определяющий направление касательной к кривой в какой-либо точке М 1. Параллельно перенеся вектор
1 – единичный вектор, определяющий направление касательной к кривой в какой-либо точке М 1. Параллельно перенеся вектор 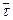 1 в точку М, проведем плоскость через векторы
1 в точку М, проведем плоскость через векторы 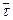 и
и 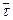 1, приложенные в точке М. Если расстояние между точками М и M1 уменьшать, устремив к нулю, то эта плоскость в пределе займет определенное положение. Полученную таким путем плоскость называют соприкасающейся плоскостью в точке М. Если рассматриваемая кривая плоская, она будет целиком расположена в соприкасающейся плоскости.
1, приложенные в точке М. Если расстояние между точками М и M1 уменьшать, устремив к нулю, то эта плоскость в пределе займет определенное положение. Полученную таким путем плоскость называют соприкасающейся плоскостью в точке М. Если рассматриваемая кривая плоская, она будет целиком расположена в соприкасающейся плоскости.
Ось, проведенная из точки М в соприкасающейся плоскости перпендикулярно к касательной к кривой в данной точке и направленная в сторону вогнутости кривой, называется главной нормалью. Ее направление принято характеризовать единичным вектором (ортом) 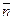 (рис. 2.7).
(рис. 2.7).
Соответственно, касательная составляющая ускорения направлена по касательной оси к траектории в данной точке, нормальная составляющая – по главной нормали (рис. 2.8), и они соответственно будут равны:
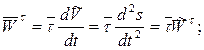 (2.13)
(2.13)
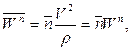 (2.14)
(2.14)
где
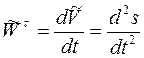 (2.15)
(2.15)
– алгебраическое значение касательной составляющей ускорения;
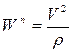 (2.16)
(2.16)
– модуль нормальной составляющей ускорения, 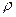 – радиус кривизны траектории в данной точке.
– радиус кривизны траектории в данной точке.
Справка: радиус кривизны кривой в данной точке равен радиусу окружности, частью которой можно заменить бесконечно малый участок кривой в окрестности данной точки с возможно большей точностью. Для окружности радиус кривизны равен радиусу окружности 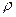 = R. Для прямой радиус кривизны в любой точке равен бесконечности
= R. Для прямой радиус кривизны в любой точке равен бесконечности 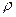 = ∞.
= ∞.
Если 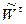 >0, то вектора
>0, то вектора 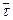 и
и 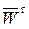 направлены в одну сторону, если
направлены в одну сторону, если 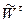 <0, то в противоположные (рис. 2.9).
<0, то в противоположные (рис. 2.9).

Рис. 2.9
Вектор ускорения 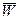 при естественном способе задания движения точки можно определить по правилу параллелограмма (рис. 2.10), соответственно его модуль будет равен:
при естественном способе задания движения точки можно определить по правилу параллелограмма (рис. 2.10), соответственно его модуль будет равен:
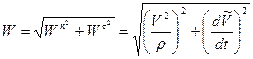 (2.17)
(2.17)
Направление вектора 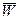 в пространстве принято характеризовать тангенсом угла φ между этим вектором и касательной осью (рис. 2.10):
в пространстве принято характеризовать тангенсом угла φ между этим вектором и касательной осью (рис. 2.10):
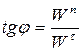 (2.18)
(2.18)
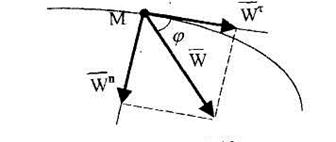
Рис. 2.10
Иногда уравнения движения точки заданы в координатной форме, а требуется определить нормальную и касательную составляющие ускорения и радиус кривизны траектории в некоторой точке. В этом случае для определения модулей нормальной и касательной составляющих удобно использовать выражения:
Wτ 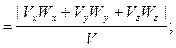 (2.19)
(2.19)
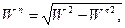 (2.20)
(2.20)
а затем определить радиус кривизны траектории по формуле:
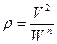 (2.21)
(2.21)
Если известно, что траектория движения точки плоская и расположена в плоскости (Oxy), то выражение (2.19) упрощается:
Wτ 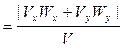 (2.22)
(2.22)
Во всем многообразии задач на кинематику точки можно выделить несколько основных типов.
1. Задачи на определение законов движения и уравнений траектории.
Они решаются в следующей последовательности:
а) выбираются система координат и точка ее начала так, чтобы
дальнейшее решение было возможно более простым;
б) на основании условий задачи для избранной системы координат
составляются уравнения движения точки, то есть находятся зависимости
координат от времени;
в) исключая из уравнений движения время, получают уравнения
траектории;
г) исследуя уравнения траектории и уравнения движения, отвечают
на различные вопросы задач.
2. Задачи на определение по заданным уравнениям движения в координатной форме траектории движения, скорости, составляющих ускорения и модуля ускорения точки, а также радиуса кривизны траектории в данной точке. Они решаются в следующей последовательности:
а) исключая время из уравнений движения, определяют уравнения траектории; если траектория движения – прямая или окружность, то радиус кривизны в любой точке этих траекторий постоянен и соответственно равен бесконечности или радиусу окружности;
б) дифференцируя координаты точки, определяют проекции вектора
скорости и ускорения на оси неподвижной декартовой системы координат
и их модули;
в) используя выражения (2.19) или (2.22), определяют модуль
касательной составляющей ускорения;
г) если радиус кривизны траектории определен по ее виду, то определяют модуль нормальной составляющей по формуле (2.16), в противном случае – по формуле (2.20);
д) если траектория движения не прямая или окружность, то определяют радиус кривизны траектории по формуле (2.21).
3.Задачи на определение уравнений движения и траектории, если ускорение движения точки задано. Они решаются в следующей последовательности:
а) выбирается система координат;
б) определяются проекции вектора ускорения на оси системы координат;
в) интегрируя полученные проекции, определяют проекции вектора скорости на оси координат;
г) интегрируя выражения для проекций скорости, определяют уравнения движения точки;
д) исключая из уравнений движения время, определяют уравнение траектории;
е) исследуют уравнение траектории.
Пример 2.1. Кривошип ОМ длиной l вращается вокруг оси, перпендикулярной плоскости рисунка и проходящей через точку О (рис. 2.11). Угол φ между неподвижной осью Ох и кривошипом изменяется по закону φ = kt, где k – некоторая постоянная величина, t –время. Необходимо: составить уравнения движения точки в декартовой системе координат, найти уравнение ее траектории, определить время одного оборота точки.
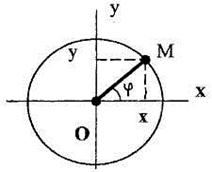
Рис. 2.11
Введем ось Оу декартовой системы координат, направив ее вверх перпендикулярно оси Ох. Координаты точки М в этой системе координат будут равны:
x = lcos φ; y = lsin φ,
или
x = lcoskt; y = lsinkt. (2.23)
Это и будут искомые уравнения движения точки М.
Чтобы найти уравнение траектории в явной форме, надо исключить из уравнений движения время. Для этого возведем каждое из уравнений (2.23) в квадрат и сложим их. Учитывая известную формулу тригонометрии, получим:
х2+у2=l2.
Следовательно, траекторией движения точки М является окружность с радиусом l и центром в начале координат.
Определим время одного оборота точки М. Это время Т, за которое угол φ изменится на 2π радиан:
φ = кТ = 2π,
откуда
Т = 2π /к.
Пример 2.2. По заданным уравнениям движения точки М х = 4t (м),
у = 16t 2 - 1 (м) установить вид ее траектории и для момента времени t=t 1 =0,5 с, найти положение точки на траектории, ее скорость, полное ускорение, касательную, нормальную составляющие ускорения, а также радиус кривизны траектории в соответствующей точке.
Для определения уравнений траектории движения точки исключим время t из уравнений движения. Для этого выразим t из уравнения для координаты х и подставим в уравнение для координаты у, получим:
у= х2-1.
Найденное уравнение есть уравнение параболы (рис. 2.12).
Подставляя t= t 1 в уравнения движения, определим координаты точки М на траектории в заданный момент времени:
x1 = 4t1 = 2 м; у1 = 16 t1 2 -1 = 3 м,
и нанесем ее на график траектории (рис.2.12).
Дифференцируя уравнения движения точки, найдем проекции вектора скорости на оси координат:
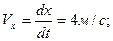
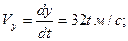 (2.24)
(2.24)
Для момента времени t= t 1 будем иметь:
Vx =4м/с; Vy= 16м/с.
Модуль скорости точки будет равен:
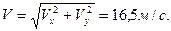
Дифференцируя уравнения (2.24), найдем проекции ускорения точки на оси координат:
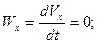
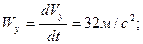
Модуль ускорения точки будет равен
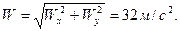
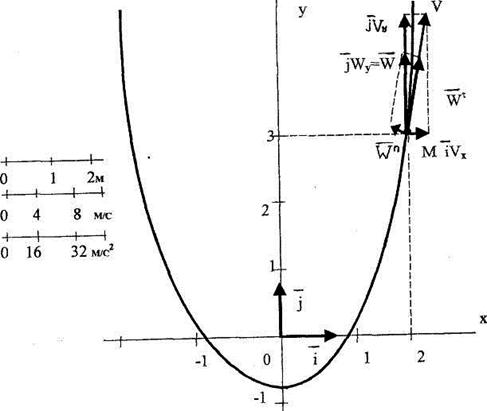
Рис. 2.12
Касательную составляющую ускорения определим, используя формулу (2.22):
Wτ 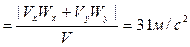 .
.
Модуль нормальной составляющей ускорения в данный момент времени будет равен
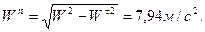
Радиус кривизны траектории в данной точке будет равен
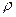 = V 2/ Wn = 34,3м.
= V 2/ Wn = 34,3м.
На графике траектории (рис. 2.12) в найденном положении точки М и в выбранном масштабе построим вектора скорости, ускорения и их составляющих.
Пример 2.3. Из пушки выстреливают снарядом со скоростью V0 под углом 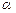 к горизонту. Вылетев из ствола, снаряд продолжает движение под действием силы тяжести, сообщающей ему вертикальное ускорение
к горизонту. Вылетев из ствола, снаряд продолжает движение под действием силы тяжести, сообщающей ему вертикальное ускорение
g = 9,8 м/с. Считая поверхность Земли горизонтальной, определить уравнение траектории движения снаряда и максимальную высоту, на которую поднимется снаряд, а также при каком значении угла 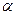 будет достигнута максимальная дальность полета.
будет достигнута максимальная дальность полета.
Так как траектория полета снаряда лежит в вертикальной плоскости, введем в рассмотрение декартову систему координат, состоящую из двух взаимно перпендикулярных осей. Начало системы координат расположим в точке вылета снаряда из ствола орудия, ось Оу направим вертикально вверх, ось Ох – горизонтально в направлении полета снаряда (рис. 2.13). Поэтому начальные условия по координатам будут нулевыми, то есть х(0)=0, у(0)=0.Время в момент вылета снаряда из ствола выберем за ноль, то есть t = to = 0. Проецируя вектор 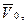 на оси координат, определим начальные условия по скорости:
на оси координат, определим начальные условия по скорости:
Vx(0) = V0cos 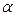 ; Vy(0) = Vosin
; Vy(0) = Vosin 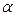 .
.
По условию задачи:
Wx = 0, Wy= - g.
Но согласно (2.12):
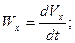
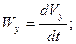
поэтому можем записать:
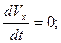
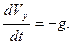 (2.25)
(2.25)
Разделяя переменные в уравнениях (2.25) и интегрируя их, получим:
Vx = C1; Vy= - gt + C2, (2.26)
где C1, C2 – постоянные интегрирования.
Подставляя в (2.26) начальные условия по времени и скорости, найдем:
С 1= Vo cos 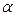 ; C2 = Vo sin
; C2 = Vo sin 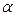 .
.
Подставляя найденные постоянные интегрирования в (2.26), получим уравнения, описывающие изменение скорости полета снаряда от времени:
Vx=V0 cos 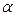 ; Vy=-gt + Vo sin
; Vy=-gt + Vo sin 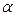 . (2.27)
. (2.27)
Но, согласно (2.3)
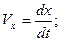
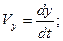
поэтому можно записать
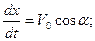
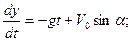 (2.28)
(2.28)
Разделяя переменные в уравнениях (2.28) и интегрируя их, получим:
x = V0 cos 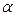 ·t + C3; y = -
·t + C3; y = - 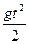 +V0 sin
+V0 sin 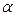 · t + C4, (2.29)
· t + C4, (2.29)
где С3, С4 – постоянные интегрирования.
Подставляя в (2.29) начальные условия по времени и координатам, найдем
С3=0; С4=0.
Подставляя найденные постоянные интегрирования в (2.29), получим уравнения, описывающие закон движения снаряда в координатной форме:
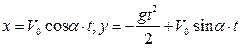 (2.30)
(2.30)
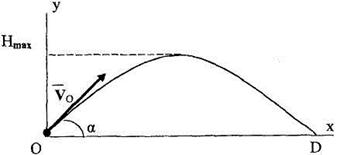
Рис. 2.13
Для определения уравнения траектории в явной форме исключим из уравнений (2.30) время. Для этого выразим t из первого уравнения (2.30) и подставим во второе, получим:
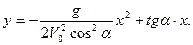
Это есть уравнение параболы (рис. 2.13).
Максимальная высота полета будет достигнута в момент изменения направления вертикальной составляющей скорости, то есть в момент t = t1, в который вертикальная составляющая скорости будет равна нулю. Приравнивая к нулю правую часть второго уравнения (2.27) и заменяя в нем t на t 1, получим
-gt1 + Vo sin 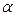 =O,
=O,
откуда
t1 = 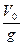 sin
sin 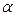 .
.
Подставляя t 1 во второе уравнение (2.30), найдем
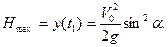
Дальность полета может быть определена как значение координаты х в момент t = t2, в который снаряд коснется поверхности Земли, то есть когда значение координаты у будет равно нулю. Заменяя в правой части второго уравнения (2.30) t на t2 и приравнивая ее к нулю, получим уравнение
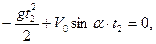
которое имеет два решения:
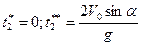
Первое решение соответствует моменту вылета снаряда из ствола, второе – достижению поверхности Земли в конце траектории. Подставляя t**2 в первое уравнение (2.30), получим
| (2.31) |
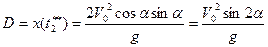
Очевидно, что правая часть (2.31) достигнет максимума при
sin2 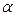 = 1, что соответствует
= 1, что соответствует 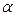 = 45°. Отсюда
= 45°. Отсюда
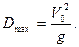
2.2. Поступательное движение твердого тела
Движение твердого тела называется поступательным, если отрезок, проведенный через две произвольные точки тела, во все время движения остается параллельным своему первоначальному положению. Так, если рассматривать тело, изображенное на рис. 2.14, то в любой момент времени отрезок АВ должен быть параллелен отрезку AoBo, где AoBo - начальное положение отрезка АВ.
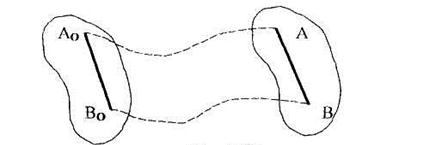
Рис. 2.14
Доказано, что при поступательном движении скорости всех точек тела равны и ускорения всех точек тела равны
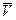 A=
A= 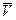 B=
B= 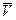 C;
C; 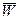 A=
A= 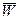 B=
B= 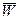 C. (2.32)
C. (2.32)
Поэтому при поступательном движении можно говорить о скорости и ускорении тела. При всех остальных видах движения этого делать нельзя.
При поступательном движении траектории точек тела, по форме повторяя друг друга, смещены относительно друг друга в пространстве. Поэтому закон поступательного движения тела можно задавать как функции x(t), y(t), z(t), описывающие изменение во времени координат какой-то одной точки тела.
Очень часто при поступательном движении траектории точек тела представляют собой параллельные прямые. В этом случае движение тела принято называть прямолинейным поступательным движением.
 2015-04-01
2015-04-01 4004
4004
