2015-10-14
844
Теорема. Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы относительно произвольного центра O равнялись нулю:
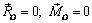. (3.4)
Доказательство
Докажем необходимость условий (3.4). Предположим, что система сил уравновешена, и приведем ее к двум силам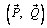 
~ 0. Тогда в соответствии с 1-й аксиомой статики эти силы должны действовать вдоль одной прямой и 
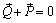. Так как 
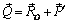, получим
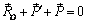, (3.5)
где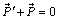 
, так как 
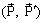– пара сил и поэтому из формулы (3.5) следует, что 
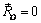. Так как силы 
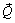и 
направлены вдоль одной прямой, линия действия последней проходит через точку O, в которой приложена сила 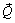(см. рис. 3.4), и поэтому главный момент
,
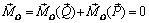т.е. необходимость доказана.
Теперь докажем достаточность. Предположим, что 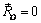и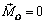 
, тогда система сходящихся сил и система пар, полученные при доказательстве теоремы Пуансо, уравновешены. Следовательно, исходная система сил эквивалентна нулю. Теорема доказана.
Спроецируем векторные равенства (3.4) на оси координатной системы Oxyz и запишем
|
|
|
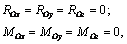
откуда с учетом (3.1) и (3.2) получим шесть уравнений равновесия пространственной системы сил:
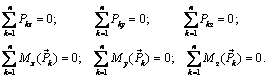(3.6)
Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил системы на каждую из трех координатных осей и суммы их моментов относительно этих осей равнялись нулю.
