2015-10-14
2511
Рассмотрим еще один способ приведения системы сил к простейшему виду.
Теорема. Произвольная пространственная система сил эквивалентна двум силам, которые в общем случае не лежат в одной плоскости.
Доказательство
Предположим, что произвольная система сил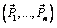 
с помощью теоремы Пуансо приведена к силе 
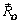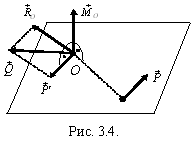
, приложенной в центре приведения O, и паре сил, момент которой 
(рис. 3.4). Выберем силы 
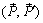, образующие пару 
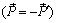, так, чтобы
,
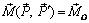приложим силу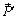 
в точке O. Затем, воспользовавшись аксиомой параллелограмма сил, сложим силы 
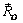и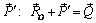 
, в результате чего получим систему двух сил 
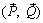, в общем случае не лежащих в одной плоскости.
Итак,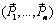 
~ 
~ 
,
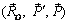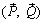а значит теорема доказана.
