Решение систем линейных алгебраических уравнений матричным методом

Рассмотрим систему из трех уравнений с тремя неизвестными (m=n):

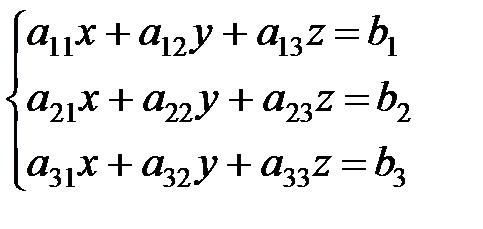
Матрица 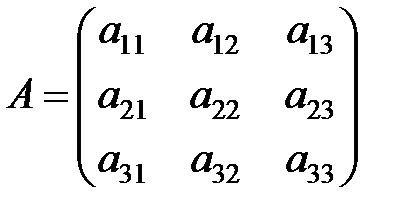, составленная из коэффициентов, стоящих перед неизвестными, называется матрицей системы или главной матрицей.

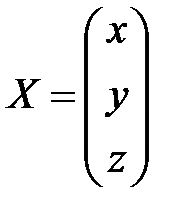- матрица-столбец неизвестных, 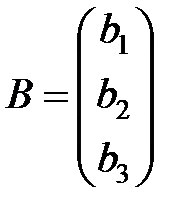- матрица-столбец свободных членов.

Систему алгебраических уравнений можно представить в виде матричного уравнения 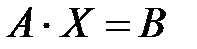. Это уравнение имеет решение, если матрица А невырожденная, т.е. 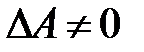. В этом случае для матрицы А существует обратная А^-1. Умножим матричное уравнение слева на матрицу А^-1.

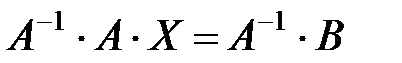, так как 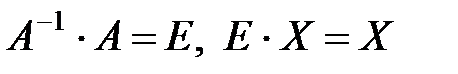, то получаем 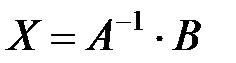- решение матричного уравнения.

Таким образом, чтобы найти матрицу неизвестных Х, надо найти обратную матрицу к главной матрице А и умножить ее на матрицу свободных членов В.

.

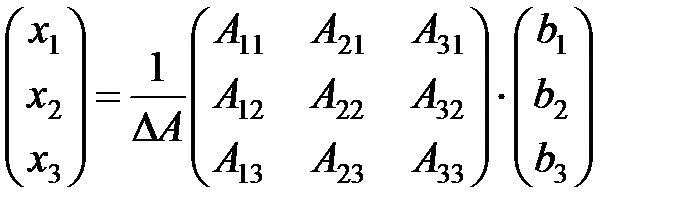Пример: Пусть дана система уравнений .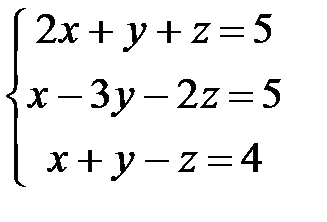

Обозначим .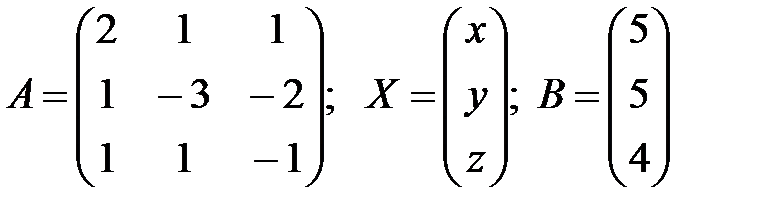

Находим определитель главной матрицы:

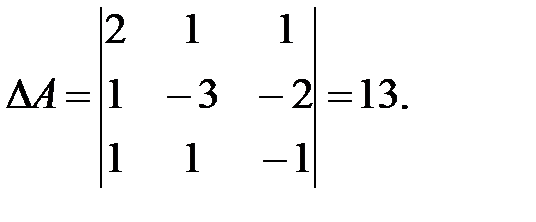
Для отыскания обратной матрицы находим алгебраические дополнения

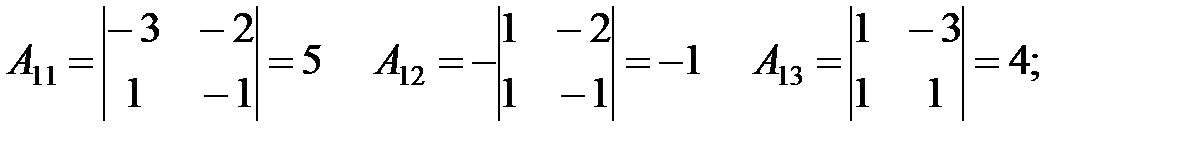
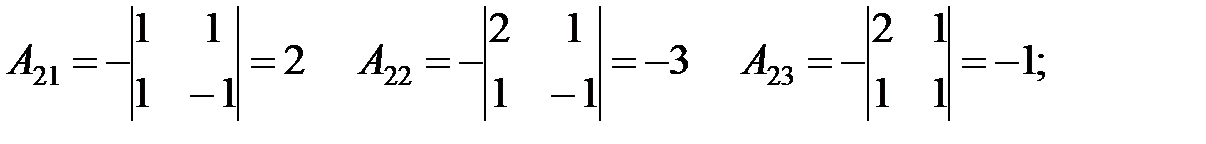
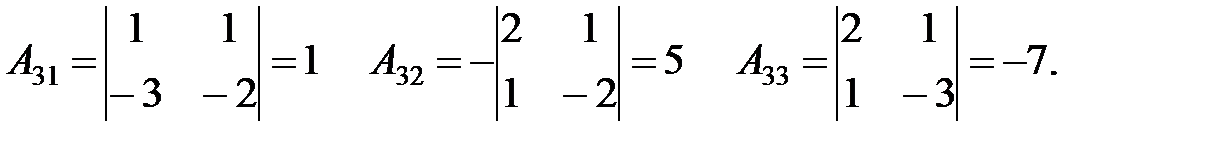
Составляем обратную матрицу

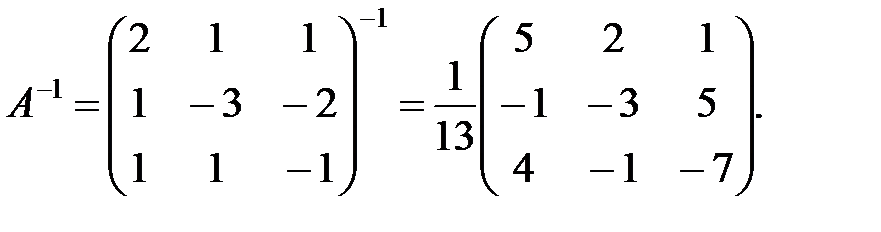
Находим неизвестную матрицу Х:

.

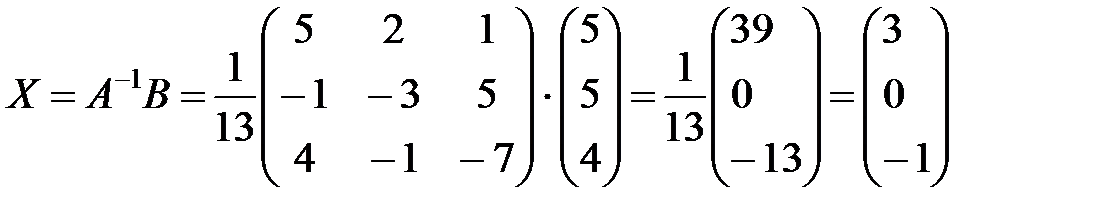Ответ: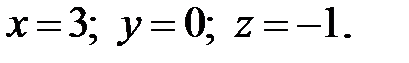

Сделаем проверку. Подставив в каждое уравнение системы полученные значения неизвестных, должны получить тождества.

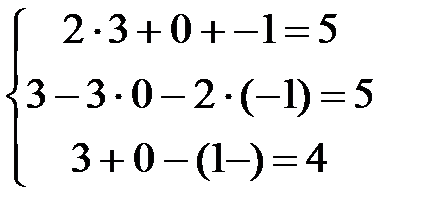
2.2 Задания для самостоятельной работы:

Найти обратные матрицы к данным, сделать проверку.

1. .

2. .

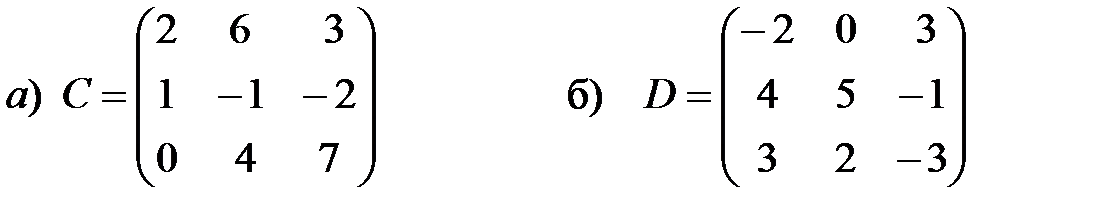3. 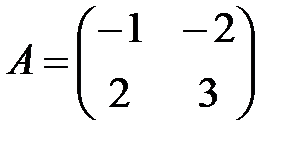. Ответ: ,

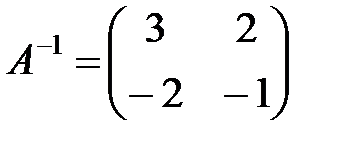4. 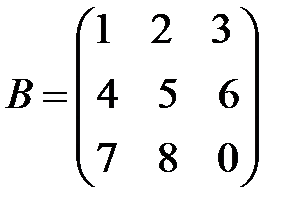. Ответ: .

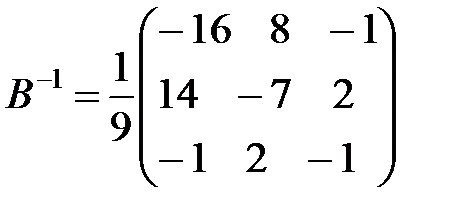Решить систему уравнений матричным методом.

1. 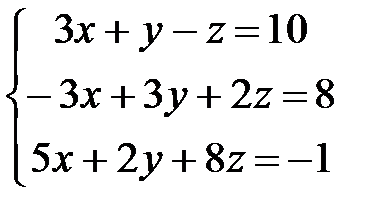Ответ: х=1; y=5; z=-2.

2.

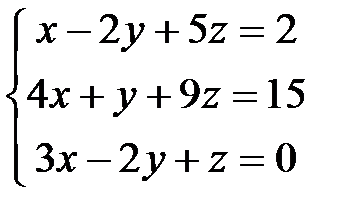
3.

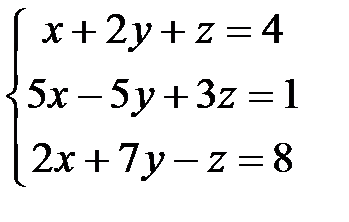
4.

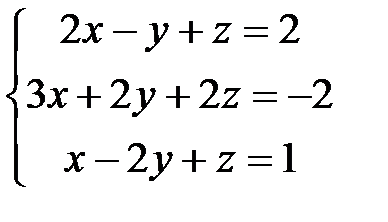
5.

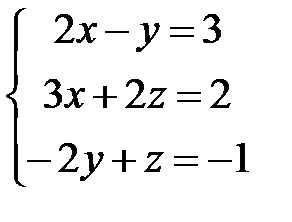
6. № 1238, № 1239, № 1240 [5]

Рекомендуемая литература: [3] стр. 522-538, [7] стр. 24, 29-30.