Уравнения системы

Линеаризация дифференциального

В реальных системах автоматического управления практически всегда наблюдаются некоторые нелинейности при преобразовании сигналов. При представлении системы с нелинейностями в виде обыкновенной линейной системы необходимо свести описание процессов в системе к обыкновенному линейному дифференциальному уравнению порядка "n". Процесс получения такого уравнения называется линеаризацией описания системы.

Используются два метода линеаризации описания системы. Первый метод применяется в том случае, когда для системы уже имеется описание процесса в виде нелинейного дифференциального уравнения. Задача состоит в преобразовании этого уравнения к линейному виду. Второй метод применим на стадии получения дифференциального уравнения при описании системы и сводится к пренебрежению нелинейными зависимостями при описании взаимосвязей между сигналами.

Рассмотрим первый метод линеаризации описания системы. Пусть в общем виде некоторая система автоматического управления описывается нелинейным дифференциальным уравнением, которое известно:

.

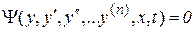Процесс в системе начинает рассматриваться с момента приложения ко входу системы внешнего воздействия. Этот момент принимается за нулевой, поэтому время рассмотрения процесса t ³ 0. В общем случае в начальный момент времени все сигналы в системе отличны от нуля и совокупность этих сигналов описывает начальное состояние системы (нулевые условия):

.

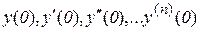Поскольку нас интересует поведение системы при t ³ 0, то исходное состояние системы может быть принято за нулевое и в дальнейшем мы можем учитывать только отклонения сигналов в системе от начальных значений. В этом случае говорят, что уравнение системы записывается в отклонениях.

Линеаризация исходного нелинейного дифференциального уравнения заключается в разложении нелинейной функции 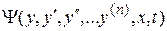в степенной ряд Тейлора и в отбрасывании членов ряда Тейлора, порождающих нелинейную зависимость. Обозначим

, ,

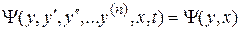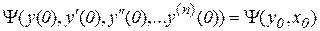тогда

.

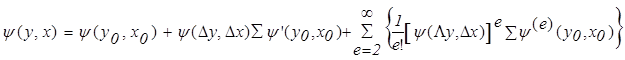При линеаризации все члены ряда Тейлора высшего порядка малости отбрасываются и принимается

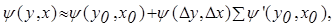
где ,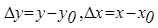

.

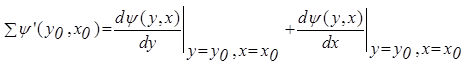В результате получаем линеаризованное дифференциальное уравнение системы "в отклонениях" (или "в вариациях")

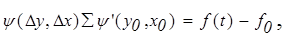
где 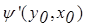- коэффициенты дифференциального уравнения.

При этом исходное дифференциальное уравнение можно переписать в виде

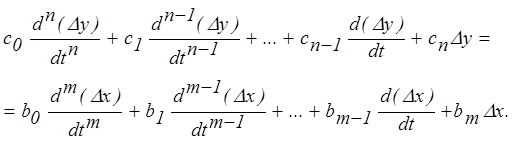
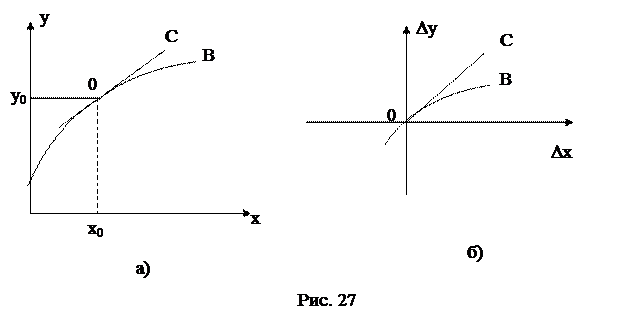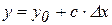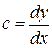Рассмотрим графическую интерпретацию проведенной линеаризации (рис. 27). На рис. 27а кривая B соответствует нелинейной зависимости y(x). Если нелинейную функцию y(x) разложить в ряд Тейлора в точке O(x₀,y₀) и отбросить нелинейные члены ряда, то кривая B будет заменена касательной C, а зависимость y(x) преобразуется к виду , где при .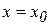

Если точку O(x₀,y₀) принять за начало координат, то получим зависимость между приращениями Δy и Δx (рис. 27б)

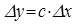, где .

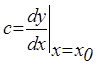В результате линеаризации исходное нелинейное дифференциальное уравнение

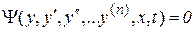
при начальных условиях 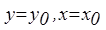можно представить в виде линеаризованного уравнения

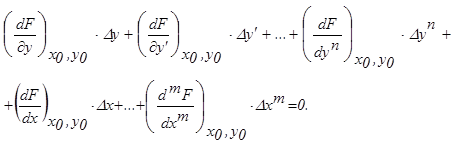
Поскольку значения производных, вычисленные при постоянных x₀, y₀, дают числовые величины, то линеаризованное уравнение можно записать в отклонениях как

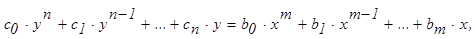
где y и x – отклонения этих величин от значений x₀ и y₀.

Пример. Рассмотрим нелинейное дифференциальное уравнение второго порядка

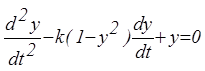, или .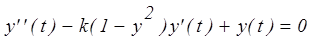

Выделим нелинейную функцию

.

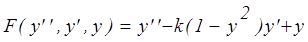Пусть начальные условия 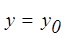, тогда

^{, ,}

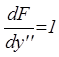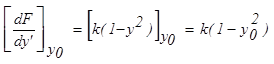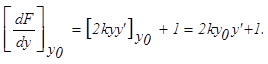
После замены нелинейной функции первыми членами ряда Тейлора получим новое приближённое уравнение

.

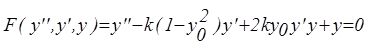Поскольку вновь полученное уравнение по-прежнему нелинейно, вторично подвергаем его линеаризации

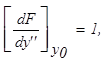
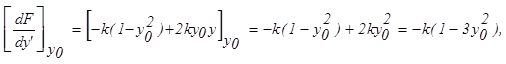
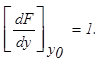
Окончательный вид линеаризованного уравнения:

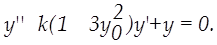
В новом уравнении 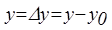, оно записано для отклонений. Это уравнение линейно.

Второй метод линеаризации заключается в том, что реальные нелинейные зависимости между сигналами уже при составлении уравнений аппроксимируются линейными зависимостями вида

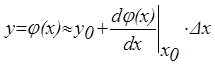
и уравнение системы изначально составляется в отклонениях:

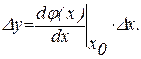
При рассмотрении обыкновенных линейных систем автоматического управления в дальнейшем рассматриваются линеаризованные дифференциальные уравнения, записанные в отклонениях. При этом везде будет подразумеваться

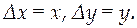
Пределы, в которых справедлива замена нелинейных дифференциальных уравнений линеаризованными, определяются допустимой величиной отклонения реальных характеристик от линеаризованных и возникающей при анализе погрешности расчета системы. Вопрос о допустимости линеаризации решается в каждом конкретном случае. Существуют случаи, когда линеаризация недопустима из-за существенного искажения реальных процессов.