Задания для самостоятельной работы

Решить систему уравнений по формулам Крамера и методом Гаусса.

1. 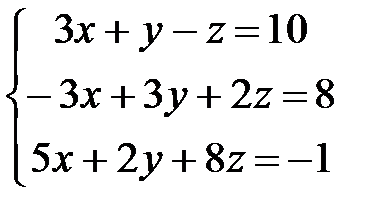Ответ: х=1; y=5; z=-2.

2.

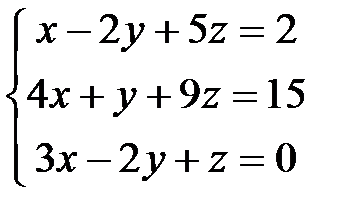
3.

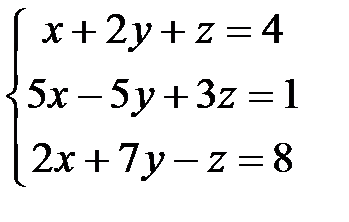
4.

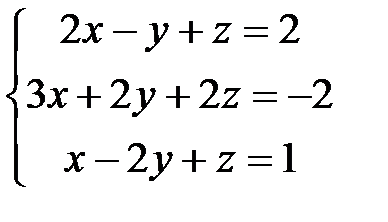
5. № 1236-1243, № 1244-1246. [5]

6. № 615 - № 622. [6]

Индивидуальная домашняя работа по теме «Системы линейных уравнений»

1. Решить систему уравнений тремя методами: с помощью формул Крамера, методами матричного исчисления, методом Гаусса. (N- номер варианта, указывает преподаватель)

а) 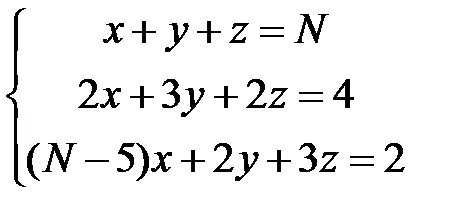б)

2. Решить систему линейных уравнений с помощью формул Крамера и методом Гаусса.

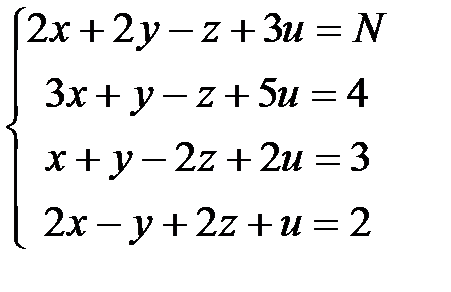
Рекомендуемая литература: [7] стр. 32-37, [4] стр. 65-69.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4

Тема: Векторы. Действия над векторами, заданными проекциями.

Краткие сведения из теории и примеры решения задач.

Векторы

Вектор – это направленный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Обозначается символом или .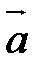

Длина отрезка АВ называется длиной или модулем вектора 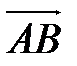и обозначается .

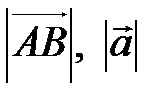Вектор, длина которого равна единице, называется единичным вектором и обозначается 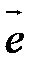. Единичный вектор называют ортом.

Два вектора называются равными, если они параллельны, направлены в одну сторону и имеют одинаковые длины.

Векторы 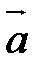и , параллельные одной и той же прямой, называются коллинеарными.

Векторы, лежащие в одной плоскости или в параллельных плоскостях, называются компланарными.