Уравнение состояния реального газа (уравнение Ван-дер-Ваальса)

Для 1 моля идеального газа уравнение состояния имеет вид 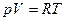, где 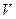- объем, предоставленный молекулам газа. Для реальных газов некоторая его часть занята самими моле­кулами. Поэтому объем 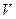надо заменить разностью .

Учтем теперь взаимодействие молекул. Силы притяжения, действующие между молекулами, приводят, к уменьшению давления газа на стенки сосуда на некоторую величину 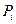, так что:

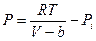или 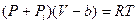(11.1)

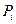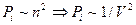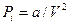где - дополнительное давление, обусловленное силами притя­жения. Его называют также внутренним или молекулярным давлени­ем. Это давление пропорционально концентрации молекул и силе, действующей на данную молекулу со стороны остальных, которая в свою очередь, также пропорциональна концентрации молекул. Таким образом, или , где 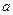- пос­тоянная, характеризующая силы молекулярного притяжения и зави­сящая от природы газа. Таким образом, получаем для 1 моля уравнение:

(11.2)

Это уравнение состояния реального газа или уравнение Ван-дер-Ваальса; 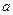и - константы, определяемые экспериментально. Исследуем уравнений (11.2), для чего перепишем его в виде:

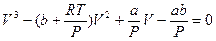(11.3)

С его помощью можно построить теоретические изотермы ре­ального газа - зависимость от 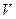при заданных значениях .

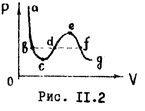
Уравнение (11.3) - уравнение третьей степени относитель­но . Поэтому оно может иметь либо три действительных корня, либо один. Одна из таких изотерм изображена на рис. 11.2. На участках , , т.е. с увеличением давления объем уменьшается, на участке же 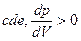, что соответству­ет неестественному состоянию вещества, когда сжатие приводит к увеличению объема. Поэтому на опыта изотерма пожег быть лишь вида 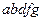(Рис. 11.3). Такая изотерма действительно была получена Т. Эндрьюсом с углекислотой. Наличии горизонтального участка связано с тем, что при изменении объема вещество не может все время оставаться в однофазном состо­янии. В некоторый момент про­исходит скачкообразной измене­ние состояния вещества и его распадение на две фазы: жидкую () и газообразную (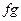). Горизонтальный участок (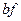) соответ­ствует двухфазному состоянию вещества - переходу газа в жид­кость при заданных температуре и давлении. Эта область насы­щенного пара.