2015-10-22
574
Каноническое уравнение прямой на плоскости: 
, где 
- направляющий вектор прямой.
Общее уравнение прямой на плоскости: 
,
где 
- вектор нормали прямой.
Уравнение прямой с угловым коэффициентом 
(рис.18), где 
- угловой коэффициент прямой; угол 
– угол между прямой и осью ОХ;
b – отрезок, отсекаемый прямой на оси OY.
Рис.18
Уравнение прямой, проходящей через две точки 
и 
: 
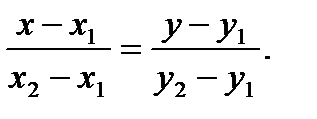
Пример Даны точки А (2;5), В (-3;1), С (5;2).
Найти: 
а) уравнение медианы AD;
б) уравнение высоты AE;
в) угол между медианой AD и высотой AE;
г) уравнение прямой, проходящей через точку С, параллельно прямой АВ (рис19).
Рис.19
Решение.
а) Точка D - середина отрезка ВС, найдем ее координаты: 
Прямая AD проходит через две точки. Её уравнение имеет вид: 
; 
;
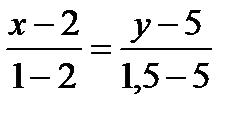- уравнение прямой AD.
б) Высота перпендикулярна ВС. Пусть точка Е имеет координаты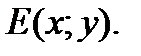 
Тогда векторы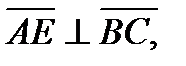 
следовательно, их скалярное произведение 
- уравнение высоты АЕ.
в) Угол 
между медианой AD и высотой АЕ – это угол между их векторами нормалей 
Отсюда, 
г) Прямая СК параллельна прямой АВ. Пусть точка K имеет координаты 
Тогда векторы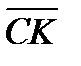 
и 
коллинеарны.
Отсюда, 
; 
; 
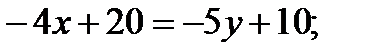
- уравнение прямой СК, параллельной АВ.
