Билет 2. Понятие ранга матрицы. Теорема о ранге матрицы

Определение. Минором порядка k матрицы A называется определитель матрицы k-го порядка, элементы которой стоят на пересечении выбранных k – строк и k – столбцов, т.е..

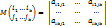
Определение. Минор порядка r матрицы A называется базисным, если он отличен от нуля, а все миноры более высокого порядка равны нулю (если они существуют)..

Определение. Рангом матрицы А называется порядок её базисного минора, т.е.. ранг матрицы A равен r, если в матрице существует ненулевой минор r-го порядка, а все миноры более высокого порядка равны нулю (если они существуют). Обозначается Rg A.

Определение. Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие базисный минор, называются базисными строками и столбцами.

Теорема о ранге матрицы. Ранг матрицы равен максимальному числу линейно независимых столбцов этой матрицы.

Доказательство. Пусть A_mxn = || a_ij ||_mxn и Rg A = k. Если А ≠ 0, то утверждение верно. Если Rg A = k =n, то утверждение верно. Если 0 < Rg A = k < n, то т.к.. Rgрядок базисного минора, то значит А содержит k базисных столбцов (они линейно независимы). Возьмем произвольные r (r > k) столбцов матрицы А. Составим матрицу В из этих столбцов. Rg B ≤ Rg A = k. По следствию 1 в этом случае столбцы матрицы B линейно зависимы. ч.т.д.

Следствие 3. Для любой матрицы А максимальное число линейно независимых столбцов равняется максимальному числу линейно независимых строк этой же матрицы.

Билет 3. Элементарные преобразования матриц. Инвариантность ранга матрицы при помощи элементарных преобразованиях. Вычисление ранга матрицы.

Определение. Элементарные преобразования:

Перестановка строк; умножение строки на число, отличное от нуля; прибавление к одной строке другой, умноженное на число; аналогичные преобразования для столбцов матрицы.

Замечание. элементарные преобразования обратимы А~В

Теорема. Если А~В, то Rg A=Rg B

Доказательство. Пусть Rg A = r А 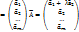=> ∃M_r≠0, а все M_r+1=0. Рассмотрим произвольный минор 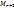в матрице

1) 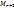не содержит левую строку, тогда 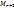=M_r+1=0

2) 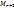не содержит второй строки 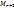=M_r+1 + λM’_r+1 = 0, M_r+1 –минор из А => M_r+1 = 0. M’_r+1 – минор матрицы А

3) 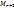содержит 1 и 2 строку. 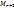= M _r+1 + λM’_r+1 = 0. M’_r+1 – совпадают 1 и 2 строки. M _r+1= M’_r+1 = 0

В все миноры 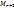= 0 => Rg ≤ r = Rg A. Т.к.. элементарные преобразования обратимы, то ~ A => Rg A ≤ Rg ≤ Rg A => Rg A = Rg ч.т.д.

Определение. Говорят, что матрица А имеет ступенчатый вид, если: 1) Ниже нулевой строки располагаются нулевые строки. 2) если a_{i 1} = … = a_{i k-1} = 0, a_{i k} ≠ 0, то a_{i k} = 1 ó ∀ s > i и ∀ t ≤ k: a_{s t} = 0

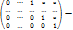ступенчатая матрица. Замечание. Ранг ступенчатой матрицы равен числу ненулевых строк.