Лабораторная работа № 8

Производная.

Опр.1. Производной функции 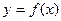по аргументу называется предел отношения приращения функции в точке к приращению аргумента при условии, что это последнее стремиться к нулю. Производная функции 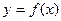обозначается .

Таким образом, по определению

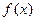Операция отыскания производной данной функции называется дифференцированием этой функции.

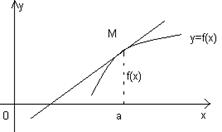
Геометрически число представляет собой угловой коэффициент касательной к графику функции 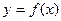в точке .

Пример 1. Исходя из определения производной, непосредственно найти производную функции у=х².

Решение:

Придадим х приращение Dх и найдем приращение функции:

Dу=у(х+Dх)-у(х)=(х+Dх)²-х²=х²+2хDх+(Dх)²-х²=2хDх+(Dх)²