2015-10-22
939
Все пять свойств, сформулированные в разделе 9.2 темы "Неопределенный интеграл" остаются без изменений для определенного интеграла. Но добавляются новые свойства, которые приведем здесь без доказательства.
1. Интеграл с постоянными пределами равен нулю 
.
2. При перестановке пределов интеграл меняет знак на противоположный
.
3. Если интервал интегрирования разбит на части, то значение интеграла на всем интервале равно сумме интегралов по каждой из составляющих частей, т.е. при любых а, b, с:
, при условии, что 
.
Заметим, что это свойство справедливо при любом числе частей, на которые разбивается интервал 
.
4. Если на интервале определены две функции 
и 
, причем 
, то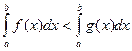 
т.е. обе части неравенства можно почленно интегрировать.
