Примеры решения задач

Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось x) имеет вид , где 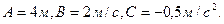Для момента времени 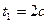определить: 1) координату х₁ точки, 2) мгновенную скорость 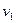, 3) мгновенное ускорение .

Решение. 1. Координату точки, для которой известно кинематического уравнение движения, найдем, подставив в уравнение движения вместо заданное значение времени :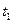

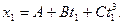
Подставим в это выражение значения А, В, С, 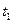и произведем вычисления: м = 4м

2. Мгновенную скорость в произвольный момент времени найдём, продифференцировав координату х по времени: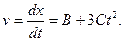

Тогда в заданный момент времени 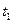мгновенная скорость Подставим сюда значения В, С, 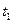и произведем вычисления: Знак минус указывает на то, что в момент времени 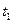=2с точка движется в отрицательном направлении координатной оси.

3. Мгновенное ускорение в произвольный момент времени найдём, взяв вторую производную от координаты х по времени: Мгновенное ускорение в заданный момент времени 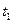равно

Подставим сюда значения С, 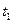и произведем вычисления: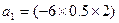

Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.

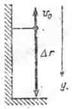Пример 2. Мячик, брошенный с балкона вер­тикально вверх, через 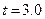с упал па Землю. Определить начальную скорость мячика, если высота балкона над Землей равна 14,1м. Сопротивлением воз­духа пренебречь.

Решение. Для решения задачи достаточно воспользоваться формулой 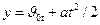, выражающей модуль пере­мещения тела.

Направим ось проекции y вертикально вниз. Соблюдая правило зна­ков, получим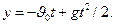

Решив уравнение относительно , найдем

Легко убедиться в том, что выбор положитель­ного направления оси отсчета произволен. Так, направив ось у вверх, получим уравнение 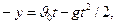которое, очевидно, равносильно предыдущему.

Пример 3. Тело брошено со скоростью 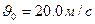под углом к горизонту. Пренебрегая сопротивлением воздуха, найти скорость тела, а также его нормальное и тангенциальное ускорения через с после начала движения. На какое рас­стояние переместится за это время тело по горизонтали и на какой окажется вы­соте .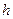

Решение. Так как тело движется с постоянным ускорением , его скорость и перемещение определяются векторными урав­нениями ,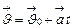

Мы не знаем, в какой точке траектории будет тело через 1,50 с после начала движения, — на восходящей или нисходящей ветвях параболы. Предположим, что оно находится в некоторой точке М на нисходящей ветви(см. рис.).

Введем координатные оси, направленные по горизонтали (Оx) и вертикали (Оу) и совместим начало координат с положением тела в начальный момент времени. Тогда, получим

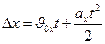
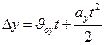
подставив в эти уравнения значения и учитывая, что проекция скорости тела в точке М на ось Оу направлена вниз, получим:

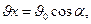
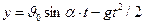
Искомые величины равны соответственно координатам х, у точки М в момент с:

Скорость 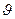в точке М найдем через ее проекции по теореме Пифагора:

Подставив числовые значения величин, получим

Для определения нормального и тангенциального ускорений учтем, что полное ускорение тела, есть не что иное как ускорение g силы тяжести. Разложив вектор и на составляющие по касательному и нормальному направлениям к траектории в токеМ, получим: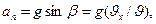

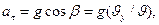
где — угол между вертикалью и касательной к траектории в точке М. Подставив вместо их значения, получим:

Вычисления дают: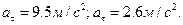

Положительное значение величины подтверждает правильность нашего предположения относительного места тела на траектории. Отрицательное значение свидетельствовало бы, что скорость тела убыва­ет и что, следовательно, оно находится на восходящей ветви параболы.

Пример 4. Маховик, вращавшийся с постоянной частотой при торможении начал вращаться, равнозамедленно. Когда торможение прекрати­лось, вращение маховика снова стало равномерным, но уже с час­тотой 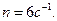Определить угловое ускорение 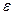маховика и про­должительность торможения, если за время равнозамедленного движения маховик сделал N =50 оборотов.

Решение. Угловое ускорение маховика связано с начальной 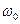и конечной 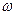угловыми скоростями соотношением откуда 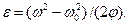Но так как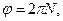 то

Подставив значения и вычислив, получим

Знак минус указывает на то, что маховик вращался замедленно.

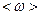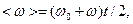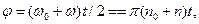Определим продолжительность торможения, используя формулу, связывающую угол поворота со средней угловой скоростью вращения и временем По условиям задачи, угловая скорость линейно зависит от времени и поэтому можно написать тогда откуда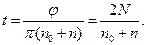

Подставив числовые значения и произведя вычисления, получим

Пример 5. Маховик вращается равноускоренно. Найти угол 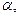который составляет вектор полного ускорения а любой точки маховика с радиусом в тот момент, когда маховик совершит первые N = 2,0 оборота.

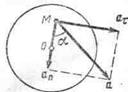
Решение. Разложив вектор а точки М на тангенциальное a_τ и нормальное a_n ускорения, видим, искомый угол опре­деляется соотношением

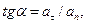
Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам, применив формулы: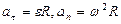

Тогда получим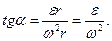

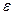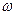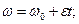
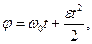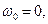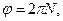Так как маховик вращается равноускоренно, найдем связь между величинами и с помощью формул равнопеременного вращения исключив из них время: Поскольку а то

Подставив значение в искомую формулу, получим

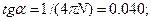
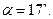
Пример 6. Движение тела массой 1 кг задано уравнением 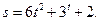Найти зависимость скорости и ускорения от времени. Вычислить силу, действующую на тело в конце второй секунды.

Решение. Мгновенную скорость находим как производную от пути по времени: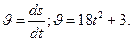

Мгновенное ускорение определяется первой производной от скорости по времена или второй производной от пути по вре­мени: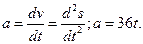

Сила, действующая на тело, определяется по второму закону Ньютона: где а- ускорение в конце второй секунды. Тогда

Ответ: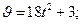

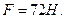
Пример 7. В лифте на пружинных весах находит­ся тело массой m=10 кг (см. рис.). Лифт движется с ускорением а =2 м/с². Определить показания, весов в двух случаях, когда ускорение лифта направле­но:

1) вертикально вверх, 2) вертикально вниз.

Решение. Определить показания весов — это значит найти вес тела G, т. е. силу, с которой тело действует на пружину. Но эта сила, по третьему закону Ньютона, равна по модулю и противо­положна по направлению силе упругости N (силе реакции опоры), с которой пружина через посредство прикрепленной к ней чашки весов действует на тело, т. е.

G=- N, или G= N.

Следовательно, задача определения показания весов сводится к нахождению реакции опоры N. В инерциальной системе отсчета на тело действуют две силы: сила тяжести Р и сила N. Направим ось z вертикально вверх и спроецируем на нее все силы, действующие на тело. Тогда: откуда Следовательно

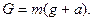
Для ускорения направленного вверх Для ускорения направленного вниз (а <0),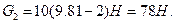

Пример 8. Определить ускорения а ₁ и а₂, с которыми движутся грузы m₁ и m₂ в установке, изображенной на рис. 2-4, а также силу натяжения Т нити. Трением и массой блоков пренебречь. Нить считать невесомой и не­растяжимой.

Решение. На груз m₁, действуют силы тяжести m₁g и сила натя­жения Т₁, нити, на груз m₁ – сила тяжести m₂g и силы натяжения Т₂, Т₃ нитей. При этом Т₁=Т₂=Т₃=Т. Поскольку все силы направлены по вертикали, запишем уравнения, выражающие второй закон Ньютона, применительно к грузам сразу в скалярном виде, выбрав положительным направление вниз и предположив, что ускорение груза m₁ направлено вниз и, следовательно, ускорение груза m₂ – вверх:

Рассматривая кинематическую схему установки и учитывая усло­вие не растяжимости нити, запишем соотношение между модулями пе­ремещений грузов, происходящих за одно и то же время: 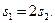Очевидно, такое же соотношение существует и между модулями уско­рений грузов: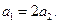

Решив совместно эти уравнения, получим:

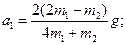
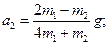
Отсюда следует: 1) если то т. е. уско­рения грузов направлены так, как мы предположили; 2) если то - грузы покоятся или движутся равномерно; 3) если 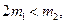то 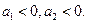В этом случае ускорение груза 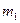направлено вверх, ускорение груза 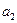- вниз.

Пример 9. Груз массой вращается на канате длиной в горизонтальной плоскости, совершая 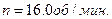Какой угол с вертикалью образует канат и какова сила его натяжения?

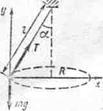
Решение. На груз действуют сила тяжести 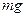и сила натяжения Т каната (см.рис.). По второму закону Ньютона, (1)

Так как движение по окружности происходит с постоянной по модулю скоростью, то полное ускорение тела равно нормальному уско­рению 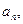направленному к центру окружности радиуса R: (2)

Выберем оси х и y так, чтобы одна из них была направлена в сторону ускорения. Проектируя на оси, получим:

Из чертежа видно, что 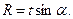Решив совместно эти уравнения, с учетом последнего равенства, имеем

Подставив числовые значения величин в единицах СИ и выполнив вычисление, находим:

Пример 10. 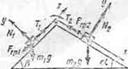На вершине двух наклонных плоскостей, образующих с горизонтом углы 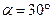и укреплен блок. Грузы и 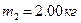соеди­нены нитью, перекинутой через блок. Определить ускорение а, с которым начнут двигаться грузы вдоль наклонных плоскостей, и силу натяжения Т нити. Коэффи­циенты трения грузов о плоскости равны между собой: Блок и нить считать невесомыми, трение в оси блока не учитывать. Рассмотретьслучаи:1) 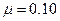2)

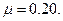
Решение. На каждый из грузов действуют четыре силы: сила тяжести, сила нормального давления N опоры, сила трения и сила натяжения Т нити. В этой задаче мы заранее не знаем направления сил трения и, следовательно, не можем сразу приступить к составлению уравнений движения грузов в скалярной форме. В самом деле, сила трения направлена всегда в сторону, противоположную относительной скорости движущегося тела. Но куда движутся грузы — неизвестно.

Воспользуемся тем, что сила трения, возникающая при движении тела, не может изменить направления его относительно ско­рости. Выясним направление движения грузов, предположив, что трение отсутствует. Так как в этом случае ускорение грузов опреде­ляется разностью составляющих сил тяжести, направленных вдоль соответствующих плоскостей, то эти составляющие:

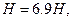
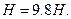
Так как 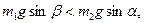то груз 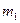будет двигаться по на­клонной плоскости вверх, груз 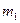- вниз. А поскольку силы трения не могут изменить направление движения тел, то и при наличии тре­ния грузы будут двигаться так же.

Теперь приступим к составлению уравнении движения грузов. Выбрав для каждого груза оси проекций х и у так, чтобы одна из осей была направлена вдоль ускорения (см.рис.), запишем для каждого груза и 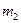в проекциях на оси соответственно по два скалярных уравнения (учитывая при этом, что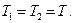

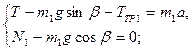
Кроме того, по закону трения скольжения,

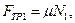
Систему уравнений с неизвестными преобразуем в систему из двух уравнений:

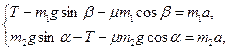
в которой два неизвестных: а и Т. Решив эту систему, получим:

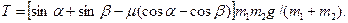
Подставив в эти формулы числовые данные для первого случая 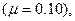получим: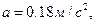

Для второго случая имеем

Прежде чем выполнять дальнейшие расчеты, проанализируем полученный результат. Отрицательное значение ускорения показывает, что при 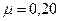направления движения грузов противоположны тем, что были бы при отсутствии трения (при этом учитываем, что в обоих случаях начальные скорости грузов равны нулю). Но этого не может быть, так как сила трения не в состоянии изменить направление движения тела. Таким образом, получен неверный ответ для ускорения. Следовательно, система уравнений не соответствует действитель­ности при 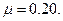Единственной ошибкой, которую мы могли здесь допустить, является предположение о том, что грузы находятся в состоянии движения и между ними и плоскостями действуют силы трения скольжения. Следовательно, на самом деле, при 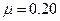грузы находятся в состоянии покоя, удерживаемые силами трения покоя, для которых соотношения несправедливы. Итак, 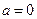при 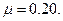Теперь вместо системы (4) получим систему

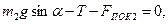
в которой неизвестны 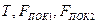и которая, очевидно, не имеет единственного решения для Т. Задача стала неопределенной: величина Т теперь зависит от некоторых дополнительных обстоятельств, не указанных в условии, а именно от того, каким образом грузы были по­мещены в положение, изображенное на рисунке.

Пример 11. Шар массой двигаясь со скоростью упруго ударяется о гладкую неподвижную стенку так, что скорость его направлена под углом 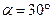к нормали. Опреде­лить импульс 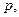получаемый стенкой.

Решение. Сначала проанализируем условие задачи. Стен­ка неподвижна, поэтому система отсчета, связанная с ней, будет инерциальной. Удар о стенку уп­ругий; следовательно, можно вос­пользоваться законом сохранения ме­ханической энергии. Из него, учи­тывая, что масса стенки, много больше массы шара, следует равенство модулей скоростей шара 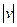до и после удара;

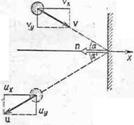Покажем, что угол отражения шара от стенки равен углу паде­ния шара. Спроецируем векторы 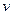и 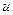на координатные оси Ох и Оу (см. рис.). Так как стенка гладкая, то 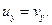Учитывая, кроме того, что получим 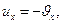а от­сюда следует равенство углов падения и отражения

Для определения импульса, полученного стенкой, воспользу­емся законом сохранения импульса. Для нашего случая этот за­кон можно записать в виде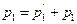

где и 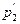- импульсы шара до и после удара .

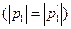Отсюда импульс, полученный стенкой,

Из рис. видно, что вектор сонаправлен с осью Ох и его модуль 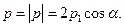Подставив сюда выражение импульса 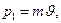получим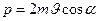

Произведем вычислия: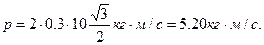

Пример 12. На железнодорожной платформе, дви­жущейся по инерции с некоторой скоростью, ук­реплено орудие, ствол которого направлен в сторону движения платформы и припод­нят над горизонтом на угол (см.рис.). Орудие произвело выстрел, в результате чего скорость платформы с орудием умень­шилась в 3 раза. Найти скорость снаряда (относительно орудия) при вылете из ствола. Масса снаряда масса платформы с орудием М.

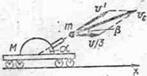Решение. На систему платформа с орудием — снаряд извне дей­ствуют две силы: сила тяжести системы и сила нормального давления N рельсов. До выстрела эти силы уравновешивались, так как система двигалась равномерно. Во время выстрела сила взаимодействия между платформой и рельсами возрастает вследствие явления отдачи, поэтому равновесие сил, приложенных к системе, нарушается: 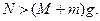Следовательно, во время выстрела система не является замкнутой, ее импульс изменяется. Учтем, однако, что обе рассмот­ренные силы действуют по вертикали, в то время как в горизонтальном направлении никакие силы на систему не действуют (трением плат­формы о рельсы пренебрегаем). Поэтому проекция импульса системы на горизонтальное направление (на ось х) есть величина по­стоянная:

Пусть состояниям системы до и после выстрела соответствуют зна­чения величины 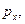равные и Рассматривая все движения отно­сительно Земли, получим:

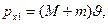
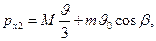
где — проекция на ось х скорости 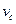снаряда относительно Земли (см.рис.).

Чтобы связать величину 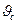с искомой скоростью будем рассмат­ривать движение снаряда относительно Земли как сложное, состоящее из двух: со скоростью 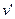относительно орудия и со скоростью 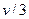вместе с орудием относительно Земли. Тогда в соответствии с законом сложения скоростей получим 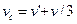Спроектируем эти векторы на ось х:

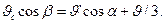
После преобразования этих уравнений получим 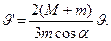Это и является ответом.

Пример 13. На спокойной воде пруда стоит лодка длиной L и массой М перпендикулярно берегу, обращенная к нему носом. На корме стоит человек массой m. На какое расстояние s приблизится лодка к берегу, если человек перей­дет с кормы на нос лодки? Трением о воду и воздух пренебречь.

Решение. Для простоты решения будем считать, что человек идет по лодке с постоянной скоростью. Лодка в этом случае так­же будет двигаться равномерно. По­этому перемещение лодки относительно берега определим по формуле

где 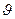— скорость лодки относительно берега; — время движения человека и лодки. Направление перемещения человека примем за положительное.

Скорость 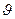лодки найдем, пользуясь законом сохранения им­пульса. Так как, по условию задачи, система человек — лодка в начальный момент была относительно берега в покое, то по закону сохранения импульса получим 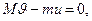где 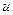—скорость человека относительно берега; знак минус указывает на то, что скорости человека и лодки по направ­лению противоположны. Отсюда

Время движения лодки равно времени перемещения человека по лодке, т. е.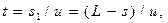

где — перемещение человека относительно берега.

Подставив полученные выражения 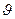и в формулу для перемещения лодки, найдем

Откуда

Заметим, что предположение о равномерности движения чело­века по лодке не является обязательным, ибо центр тяжести системы не изменит своего положения.

Пример 14. Тело массой 1 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от време­ни задана уравнением Определить работу силы за 10с с начала ее действия и зависимость кинетической энергии от времени.

Решение. Работа, совершаемая силой, выражается через криволи­нейный интеграл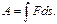

Сила, действующая на тело, по второму закону Ньютона равна 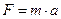или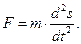

Мгновенное значение ускорения определяется первой произ­водной от скорости по времени или второй производной от пути по времени. В соответствии с этим находим

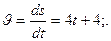
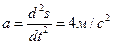
Тогда Определив 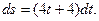и подставив эти выражения в формулу для работы, получим

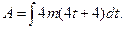
По этой формуле работа, совершаемая силой за 10с с начала ее действия:

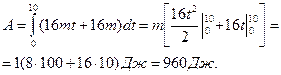
Кинетическая энергия определяется по формуле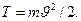

Подставляя сюда выражение для скорости, имеем

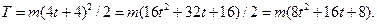
Ответ:

Пример 15. На двух нитях одинаковой длины, равной 0,8м, подвешены два свинцовых шара массами 0,5 и 1 кг. Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол 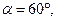и отпустили. На какую высоту поднимутся оба шара после столкновения? Удар считать цент­ральным и неупругим. Определить энергию, израсходованную на деформацию шаров при ударе.

Решение. Так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью 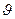. Закон сохранения импульса при этом ударе имеет вид

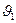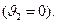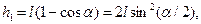Здесь и - скорости шаров до удара. Скорость большого шара до удара равна нулю Скорость меньшего шара найдем, используя закон сохранения энергии. При отклонении меньшего шара на угол ему сообщается по­тенциальная энергия, которая затем переходит в кинетическую: Таким образом, по­этому

Из уравнений (1) и (2) находим скорость шаров после удара:

Кинетическая энергия шаров после удара переходит в потенциальную: где 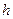— высота поднятия шаров после столкновения. Выразив 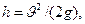с учетом преобразований получим,

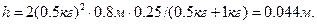
При неупругом ударе шаров часть энергии расходуется на их деформацию. Энергия деформации определяется разностью ки­нетических энергий до и после удара:

После преобразований получим

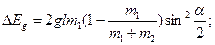
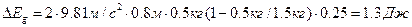Ответ:

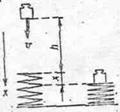Пример 16. Гиря, положенная на верхний конец спиральной пружины, сжимает ее на 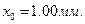На сколько сожмет пружину эта же гиря, брошенная вертикально вниз с высоты со скоростью ?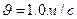

Решение. Искомая величина деформации пружины опреде­ляет из формулы для потенциальной энергии тела 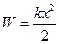. Поэтому вос­пользуемся законом сохранения энергии. Так как на гирю действует сила тяжести, рассмотрим систему Земля-гиря-пружина. По­скольку при движении гири и сжатии пружины трения практически не возникает, полная механическая энергия этой изолированной си­стемы будет сохраняться.

Посчитаем энергию системы в ее начальном (I) и конечном (II) положениях (см.рис.). Выберем за нулевой уровень отсчета высоты самое нижнее положение гири, соответствующее сжатой пружине. В начальном положении энергия системы складывается из потенциальной и кинетической энергии гири: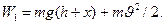

В конечном положении у гири не будет кинетической энергии, зато сжатая пружина будет обладать энергией упругой деформации. Теперь полная энергия системы будет равна: 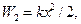где коэффициент упругости из условия равновесия тела, расположенного на пружине, равен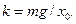

Приравнивая по закону сохранения энергии, правые части выражений для энергии с учетом последнего соотношения, получим квадратное уравнение относительно :

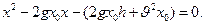
Решив уравнение, найдем

Отрицательный корень уравнения должен быть отброшен: 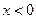означает растяжение пружины, тогда как на самом деле она сжимается. Подстановка величин в единицах СИ дает:

Пример 17. Боёк (ударная часть) свайного молота массой падает на сваю массой со скоростью Определить: 1) кинетическую энергию 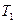бойка в момент удара; 2) энергию 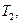затраченную на углубление сваи в грунт; 3) кинети­ческую энергию перешедшую во внутреннюю энергию системы; 4) КПД 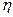удара бойка о сваю. Удар бойка о сваю рассматривать как неупругий.

Решение. 1. Кинетическую энергию бойка в момент удара о сваю находим по формуле 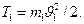Подставив значения 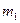и 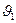, получим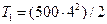

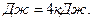
2. Чтобы определить энергию, затраченную на углубление сваи, предварительно найдем скорость системы боек—свая непосредственно после удара. Для этого применим закон сохранения импульса, который в случае неупругого удара в проекции на ось выражается формулой

где — скорость сваи перед ударом; 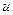— скорость бойка и сваи непосредственно после удара. Свая перед ударом находилась в состоянии покоя, поэтому 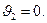Так как удар неупругий, то боек и свая после удара движутся как одно целое, т. е. с одинаковой скоростью Из последней формулы найдем эту скорость: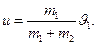

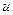В результате сопротивления грунта скорость бойка и сваи после удара быстро гасится, а кинетическая энергия, которой обладает система боек—свая, затрачивается на углубление сваи в грунт. Эту энергию находим по формуле Заменим скорость ее выражением: или, учитывая, что запишем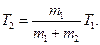

После подстановки получим

3. Боек до удара обладал энергией 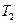- энергия, затра­ченная на углубление сваи в грунт. Следовательно, во внутреннюю энергию, связанную с неупругой деформацией сваи, превратилась энергия 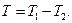Подставив в это выражение значения 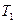и 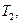найдем

4. Свайный молот служит для забивки сваи в грунт; следова­тельно, энергию 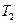следует считать полезной. КПД удара бойка о сваю выразится как отношение энергии 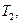затраченной на уг­лубление сваи в грунт, ко всей затраченной энергии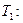 Подставив в это выражение формулу для 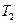, получим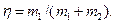

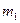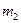Подстановка значений и дает: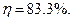

Пример 18. Маховик массой 4 кг вращается с частотой 720 мин^-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика можно считать равномерно распределенной по его ободу радиусом 40 см. Через 30 с под действием тормозящего момента маховик остановился. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.

Решение. Для определения тормозящего момента М сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения:

где 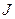— момент инерции маховика относительно оси, проходя­щей через центр масс; 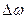— изменение угловой скорости за промежуток времени

По условию, 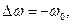где 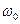— начальная угловая скорость, так как конечная угловая скорость Выразим начальную угловую скорость через частоту вращения маховика; тогда 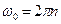и Момент инерции маховика 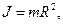где 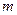-масса маховика; 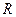- его радиус. Формула основного уравнения динамики вращательного движения прини-

мает вид 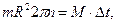откуда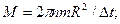

Угол поворота за время вращения маховика до остановки может быть определен по формуле для равнозамедленного вращения: где 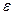— угловое ускорение.

По условию, Тогда 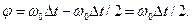Так как то число полных оборотов

Ответ: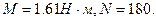

Пример 19. Тонкий стержень массой 300 г и длинной 50 см вращается с угловой скоростью 10 с^-1 в горизонтальной плоскости вокруг вертикальной оси, преходящей через середину стержня. Найти угловую скорость, если в процессе вращения в той же плоскости стержень переместится так, что ось вращения пройдет через конец стержня.

Решение. Используем закон сохранения момента количества движения 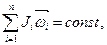где 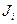— момент инерции стержня относительно оси вращения. Для изолированной системы тел векторная сумма моментов количества движения остается постоянной. В данной задаче всле­дствие того, что распределение массы стержня относительно оси вращения изменяется, момент инерции стержня также изменится. Тогда в соответствии с законом сохранения момента количества движения

запишем

Известно, что момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню, равен 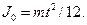По теореме Штейнера,

где 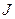— момент инерции тела относительно производной оси вращения; — момент инерции относительно параллельной оси, проходящей через центр масс; 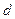— расстояние от центра масс до выбранной оси вращения.

Найдем момент инерции относительно оси, проходящей через его конец и перпендикулярной стержню:

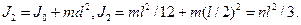
Подставляя в полученные уравнения в закон сохранения момента импульса, получим:

Откуда 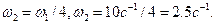Ответ:

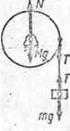Пример 20. На горизонтальную ось насажен шкив радиуса R. На шкив намотан шнур, к свободному концу которого подвесили гирю массой 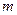. Считая массу М шкива равномерно распределенной по ободу, оп­ределить ускорение с которым будет опускаться гиря, силу натяжения Т нити и силу давления шкива на ось.

Решение. Поскольку ускорение центра инерции шкива 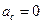и шкив только вращается, уравнения движения для него запишутся к виде

а) 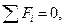б)

На шкив действуют силы тяжести натяжения Т нити и реак­ции N оси. Последняя по третьему закону Ньютона численно равна искомой силе давления шкива на ось. Очевидно, сила N направлена вертикально вверх, так как только в этом случае может выполняться соотношение а). Так как все три вектора коллинеарны (т. е. параллельны одной и той же прямой), условие а) можно записать в ска­лярном виде:

Шкив вращается под действием лишь момента силы Т. Следовательно, уравнение б) будет иметь вид: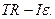

Момент инерции шкива, поскольку его масса распределена по ободу, найдем по формуле:

Эти уравнения, описывающие движение шкива, содержат три неизвестных: Т, N и Недостающее уравнение запишем, применив второй закон Ньютона для поступательного движения гири: Поскольку шнур сматывается со шкива без проскальзывания, ускоре­ние гири равно линейному ускорению точек на ободе шкива. Следовательно,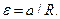

Решая совместно эту систему уравнений, найдем все три неизвестные величины:

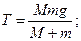
Пример 21. Через блок в виде диска, имеющий массу перекинута тонкая гибкая нить, к концам которой подвешены грузы массам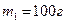и и 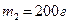(см.рис.). С каким ускорением бу­дут двигаться грузы, если их предоставить самим себе? Трением пренебречь.

Решение. Применим к решению задачи основные законы поступательного и вращательного движения. На каждый из движу­щихся грузов действуют две силы: сила тяжести 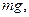направленная вниз, и сила Т натяжения нити, направленная вверх.

Так как вектор ускорения а груза 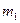направлен вверх, то Равнодействующая этих сил вызывает равноускоренное дви­жение и, по второму закону Ньютона, равна от­куда

Вектор ускорения а груза 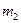направлен вниз следовательно, Запишем формулу второго закона для этого груза: 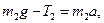откуда

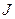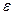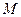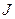
Согласно основному закону динамики вращательного движе­ния, вращающий момент М, приложенный к диску, равен произ­ведению момента инерции диска на его угло­вое ускорение : = 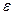. Определим вращающий момент. Силы натяже­ния нитей действуют не только на грузы, но и на диск. По третьему закону Ньютона, силы и 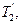приложенные к ободу диска, равны соответственно силам 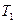и 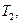но по направлению им противопо­ложны. При движении грузов диск ускоренно вращается по часовой стрелке; следовательно, 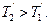Вращающий момент, приложенный к дис­ку, равен произведению разности этих сил на плечо, равное радиусу диска, т. е. Момент инерции диска <