Операционное исчисление

Задача 1. Найти оригинал функции.

№	Условие	Ответ
1.1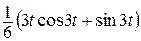
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9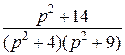
1.10

Задача 2. Операционным методом решить дифференциальное уравнение.

№	Условие	Ответ
2.1.	,	.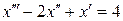
2.2	,	.
2.3	,	.
2.4	,	.
2.5	,	.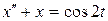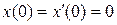
2.6	, .	.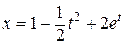
2.7	,	.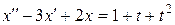
2.8	, .	.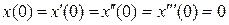
2.9	,	.
2.10	,	.

Задача 3. Операционным методом решить систему дифференциальных уравнений.

№	Условие	Ответ
3.1.
3.2
3.3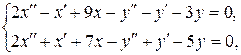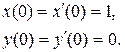
3.4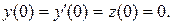
3.5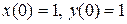
3.6	.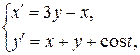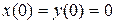
3.7
3.8
3.9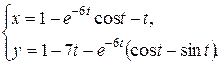
3.10

Теория вероятностей

Задача 4. В налоговую инспекцию за один день поступило n платежей, из них m налоговых платежей (остальные - не налоговые). Наудачу отобрали k платежей. Определить вероятность того, что среди них s налоговых платежей.

Вариант
n m k s

Задача 5. В двух партиях процентов качественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:

1) два бракованных; 2) ни одного бракованного; 3) одно бракованное; 4) хотя бы одно бракованное изделие.

Вариант
k1 k2

Задача 6. В квадрат с вершинами (0, 0), (0, 2), (2, 0), (2, 2) наудачу брошена точка М. Координаты точки обозначим (х, у). Найти вероятность события А, если А – область, координаты точек которой удовлетворяют указанному неравенству. Предполагается, что вероятность попадания в область, лежащую целиком внутри квадрата, зависит лишь от площади этой области и пропорциональна ей.

Вариант	Событие А	Вариант	Событие А

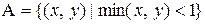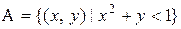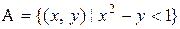Задача 7. На автозаправочную станцию поступает бензин от трех компаний, причем i -я компания поставляет k_i % бензина (i =1,2,3), из которого m_i% доброкачественного. Для лабораторных исследований сделали закупку бензина. Он оказался некачественным. Определить наиболее вероятного поставщика некачественного бензина.

Вариант
k1 k2 k3 m1 m2 m3

Задача 8. Доля елей в питомнике, имеющих нетоварный вид, составляет а %. Случайным образом отбирается п ёлок. Какова вероятность того, что число ёлок, имеющих нетоварный вид, окажется не более k?

Вариант
а п k

Задача 9. В городском казначействе правильно оформленные платёжные поручения составляют a%. Какова вероятность того, что из n платёжных поручений число правильно оформленных окажется не менее и не более ? Найти наивероятнейшее число 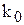правильно оформленных платёжных поручений и вычислить соответствующую вероятность.

Вариант
a n

Задача 10. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна р. Поступило п вызовов. Определить вероятность: 1) k сбоев; 2) не более k сбоев.

Вариант
р п k	0,006	0,01	0,01	0,01	0,01	0,01	0,01	0,01	0,01	0,01

Задача 11. (варианты 1–20) Дана дискретная случайная величина Х. Составить закон её распределения. Найти:

1) функцию распределения F(x), построить её график;

2) математическое ожидание М(Х);

3) дисперсию D(X) и среднее квадратическое отклонение s(Х).

Построить полигон данного распределения.

11.1. Имеется десять билетов в театр, семь из которых - на места в партере. Наудачу взяли три билета. Случайная величина Х - число билетов в партер.

11.2. Вероятность отказа детали за время испытания на надёжность равна 0,1. Случайная величина Х - число отказавших деталей среди трёх испытываемых.

11.3. В билете три задачи. Вероятность правильного решения студентом первой задачи равна 0,9, второй - 0,8, третьей - 0,7. Случайная величина Х - число правильно решенных задач в билете.

11.4. В пачке 20 накладных, 6 из которых оформлено неправильно. Наудачу взяли четыре накладные. Случайная величина Х - число накладных, оформленных неправильно.

11.5. В среднем по 10% договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Случайная величина Х - число таких договоров среди наудачу выбранных четырёх.

11.6. Вероятность того, что брокер заключит сделку с фирмой, равна 0,5. Случайная величина Х - число заключённых сделок с тремя фирмами.

11.7. Вероятность того, что сотрудник фирмы получит зарплату выше 500 усл.ед. равна 0,3. Отобрали трёх сотрудников. Случайная величина Х - количество среди отобранных сотрудников, получивших зарплату выше 500 усл.ед.

11.8. В коробке 15 конфет, 7 из которых - с коньяком. Случайная величина Х - число конфет с коньяком среди четырёх взятых.

11.9. Рабочий обслуживает два станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,8. Для второго станка эта вероятность равна 0,9. Случайная величина Х - число станков, которые не потребуют внимания рабочего в течение часа.

11.10. В рекламных целях торговая фирма вкладывает в каждую сотую единицу товара приз размером 10 рублей. Случайная величина Х - размер выигрыша при трёх сделанных покупках.

Задача 12. Непрерывная случайная величина Х - энергозатраты (усл. ед.) нескольких предприятий РАО ЕС - задана функцией распределения F(x). Найти: 1) плотность распределения вероятностей f(х); 2) математическое ожидание М(Х); 3) дисперсию D(Х) и среднеквадратическое отклонение s(Х); 4) вероятность попадания значения случайной величины Х в заданный интервал (а,b). Дать экономическое истолкование полученных числовых характеристик. Построить графики функций F(x) и f(x).

12.1 F(x) = а = 1, b = 3.

12.2 F(x) = а = 0, b = 1.

12.3 F(x) = 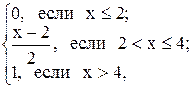а = 1, b = 3.

12.4 F(x) = 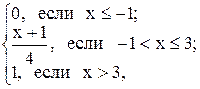а = 0, b = 2.

12.5 F(x) = 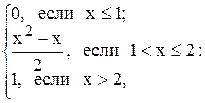, а = 1, b = 3.

12.6 F(x) = а = 0, b = 1

12.7 F(x) = а = 1, b = 3.

12.8 F(x) = а =0, b = 4.

12.9 F(x) = а = 1, b = 2,5.

12.10 F(x) = а = 1, b = 3.

Задача 13. Цена некой акции есть случайная величина, распределённая по нормальному закону. Средняя цена акции (математическое ожидание) равна а усл.ед., среднее квадратическое отклонение - s усл.ед. Найти:

1. вероятность того, что цена акции не ниже a усл.ед. и не выше b усл.ед.;

2. вероятность того, что цена акции ниже a усл.ед.;

3. вероятность того, что цена акции выше b усл.ед.;

4. вероятность того, что цена акции отклонится от средней цены не больше, чем на d усл.ед.;

5. интервал, симметричный относительно математического ожидания, в границах которого стоит ожидать цену акции с надёжностью g.

Вариант
а s a b d g	2,5 0,9	2,4 0,95	3,3 0,97	1,6 0,99	1,5 0,97	1,2 0,99	3,2 0,95	7,5 0,9	1,4 0,99	3,5 0,9