Первая основная позиционная задача

Содержание: построить на комплексном чертеже точку пересечения прямой l с плоскостью, заданной ΔАВС и определить видимость прямой относительно плоскости АВС на плоскостях П₁ и П₂ (рис. 57).

Рис. 57

Алгоритм графического решения задачи состоит из следующих элементарных операций:

1) Через данную прямую провести вспомогательную плоскость, в большинстве случаев проецирующую. Проведем в данном случае фронтально-проецирующую плоскость Σ, тогда Σ₂ = l₂.

2) Построить линию пересечения MN данной плоскости АВС и вспомогательной Σ. Прямая MN определяется точками М и N пересечения сторон АС и СВ треугольника АВС с проецирующей плоскостью Σ. ( 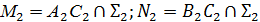). По линиям связи находим горизонтальные проекции М₁ и N₁ точек на А₁С₁ и В₁С₁. Соединив точка М₁ и N₁ прямой, получим горизонтальную проекцию линии пересечения.

3) Определить точку К пересечения прямой l с линией МN (К₁ = l₁ 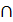М₁N₁; К₂ = М₂N₂ 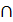К₁К₂).

4) Определить видимость. Определение видимости проводится методом конкурирующих точек.

Возьмем две точки 1 и 2, лежащие на одной горизонтально-проецирующей прямой (рис. 58). Горизонтальные проекции 1 и 2 этих точек совпадают.

Рис. 58 Рис. 59

Так как высота точки 1 больше, чем высота точки 2, т.е. 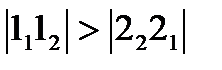, то точка 1₁ на горизонтальной проекции будет видимая, а точка 2₁ – невидимая. Берем ее в скобки. Точка 1 в пространстве лежит ближе к наблюдателю. Аналогично, возьмем две точки 3 и 4, лежащие на одной фронтально-проецирующей прямой (рис. 59). Фронтальные проекции 3₂ и 4₂ этих точек совпадают. Определим, какая из них видимая. Так как глубина точки 4 больше, чем глубина точки 3, т.е. 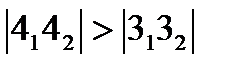, то фронтальная проекция 4₂ точки 4 видимая. Точка 4 в пространстве лежит ближе к наблюдателю. Фронтальную проекцию 3₂ точки 3 берем в скобки. Такое определение видимости называется методом конкурирующих точек, так как точки, лежащие на одной проецирующей прямой, называются конкурирующими.