Вектор (матрица-столбец) X называется собственным вектором матрицы A, если существует такое число  , что
, что
 (1.6.1)
(1.6.1)
Число  при этом называется собственным значением матрицы A, соответствующим вектору X.
при этом называется собственным значением матрицы A, соответствующим вектору X.
Равенство (1.6.1) можно записать в виде 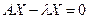 или
или
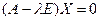 (1.6.2)
(1.6.2)
Полученное матричное уравнение представим в виде однородной системы линейных уравнений
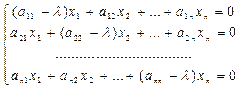 (1.6.3)
(1.6.3)
Эта однородная система всегда имеет нулевое решение X=(0,0,…,0). Чтобы получить ненулевое решение необходимо найти собственные значения матрицы A из решения характеристического уравнения
 (1.6.4)
(1.6.4)
и с каждым из них решить однородную систему (1.6.3).
Пример 1.6.1. Найти собственные значения и собственные векторы матрицы
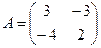
Решение: составляем характеристическое уравнение
 или
или 
и находим собственные значения матрицы A.

1) Для собственного значения  однородная система (1.6.3) имеет вид
однородная система (1.6.3) имеет вид
 или
или 
Полученная система эквивалентна одному уравнению  и имеет множество решений вида
и имеет множество решений вида  или
или  - собственный вектор матрицы A, соответствующий собственному значению
- собственный вектор матрицы A, соответствующий собственному значению  .
.
2) Для собственного значения  однородная система (1.6.3) имеет вид
однородная система (1.6.3) имеет вид
 или
или 
Полученная система эквивалентна одному уравнению 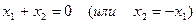 и имеет множество решений вида
и имеет множество решений вида  или
или  - собственный вектор матрицы A, соответствующий собственному значению
- собственный вектор матрицы A, соответствующий собственному значению  .
.
Ответ: 1)  - собственный вектор матрицы A, соответствующий собственному значению
- собственный вектор матрицы A, соответствующий собственному значению  , 2)
, 2)  - собственный вектор матрицы A, соответствующий собственному значению
- собственный вектор матрицы A, соответствующий собственному значению  .
.
 Задача 1. Найти собственные векторы и собственные значения матриц
Задача 1. Найти собственные векторы и собственные значения матриц
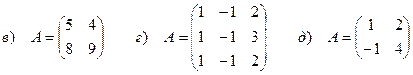
 2015-10-22
2015-10-22 1495
1495
