Алгебраическим дополнением  к элементу
к элементу  квадратной матрицы
квадратной матрицы  размерности
размерности  называется произведение числа
называется произведение числа  и определителя, полученного из определителя матрицы
и определителя, полученного из определителя матрицы  путем вычеркивания строки с номером
путем вычеркивания строки с номером  и столбца с номером
и столбца с номером  .
.
Пример 1.4.1. Найти алгебраическое дополнение  матрицы
матрицы

 Решение: матрица А имеет размерность 4×4, ее элемент
Решение: матрица А имеет размерность 4×4, ее элемент  . Найдем алгебраическое дополнение
. Найдем алгебраическое дополнение  по определению, умножая на число
по определению, умножая на число  определитель, полученный из определителя матрицы А путем вычеркивания 2-ой строки и 3-его столбца, т.е.
определитель, полученный из определителя матрицы А путем вычеркивания 2-ой строки и 3-его столбца, т.е.

Δ
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля.
Любая невырожденная квадратная матрица имеет обратную матрицу 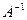 , которая находится по формуле
, которая находится по формуле
 (1.4.1)
(1.4.1)
Обратная матрица обладает следующим свойством  , которое служит для проверки правильности вычисления обратной матрицы (здесь Е – единичная матрица).
, которое служит для проверки правильности вычисления обратной матрицы (здесь Е – единичная матрица).
Пример 1.4.2. Найти обратную матрицу к матрице А и сделать проверку

Решение: найдем определитель матрицы А

 .
.
 Так как определитель матрицы
Так как определитель матрицы  отличен от нуля, то матрица А является невырожденной, у нее существует обратная матрица
отличен от нуля, то матрица А является невырожденной, у нее существует обратная матрица 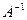 . Вычислим алгебраические дополнения элементов матрицы
. Вычислим алгебраические дополнения элементов матрицы




 Тогда обратная матрица согласно формуле (1.4.1) имеет вид
Тогда обратная матрица согласно формуле (1.4.1) имеет вид
Обратная матрица найдена, сделаем проверку (произведение матриц описано в параграфе 1.1).

Следовательно, обратная матрица найдена верно.
Ответ:  Δ
Δ
С помощью обратной матрицы возможно решение систем линейных уравнений. Рассмотрим систему n линейных уравнений c n переменными общего вида
 (1.4.2)
(1.4.2)
Обозначим матрицы

Тогда систему линейных уравнений (1.4.2) можно записать в виде матричного уравнения
 . (1.4.3)
. (1.4.3)
Решение полученного уравнения можно найти, умножив обе части уравнения слева на 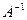

Используя свойство  обратной матрицы, получим
обратной матрицы, получим

или  - решение матричного уравнения (1.4.3).
- решение матричного уравнения (1.4.3).
Такой метод решения систем линейных уравнений получил название матричного метода или метода матричного исчисления. Кроме уравнения (1.4.3) существуют другие матричные уравнения:
 (1.4.4)
(1.4.4)
и  . (1.4.5)
. (1.4.5)
 Для решения уравнения (1.4.4) следует умножить уравнение справа на матрицу
Для решения уравнения (1.4.4) следует умножить уравнение справа на матрицу 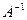 :
:
-
решение матричного уравнения (1.4.4).
Пример 1.4.3. Решить систему линейных уравнений матричным методом

Решение: обозначим матрицы
 Тогда систему линейных уравнений можно записать в виде
Тогда систему линейных уравнений можно записать в виде  , а ее решение по матричному методу находится в виде
, а ее решение по матричному методу находится в виде  . Для определения обратной матрицы
. Для определения обратной матрицы 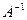 вычислим определитель матрицы А и алгебраические дополнения ко всем ее элементам
вычислим определитель матрицы А и алгебраические дополнения ко всем ее элементам






По формуле (1.4.1) получим обратную матрицу

и решение матричного уравнения
 или
или 
Ответ: (2,-3,1) □
Задача 1. Найти обратную матрицу 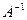 и сделать проверку:
и сделать проверку:

Задача 2. Решить систему линейных уравнений матричным методом

 Задача 3. Решить матричное уравнение
Задача 3. Решить матричное уравнение
 2015-10-22
2015-10-22 7467
7467
