Общее уравнение плоскости. Нормальный вектор.
Прямая в пространстве: канонические, параметрические уравнения.
1. Записать общее уравнение плоскости.
2. Что определяют в пространстве 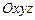 (точку, прямую, плоскость) приведенные ниже уравнения:
(точку, прямую, плоскость) приведенные ниже уравнения:
а)  ; б)
; б) 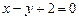 ; в)
; в)  ; г)
; г) 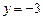 ; д)
; д)  .
.
Какую геометрическую информацию можно извлечь из приведенных уравнений?
3. Записать общее уравнение координатных плоскостей  .
.
4. Найти уравнение плоскости, проходящей через три точки 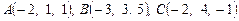 .
.
5. Найти уравнение плоскости  , проходящей через точку
, проходящей через точку 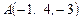 параллельно плоскости
параллельно плоскости 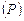 :
:  .
.
6. Найти двугранный угол, под которым пересекаются плоскости  и
и 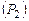 .
.
 :
:  ,
, 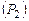 :
: 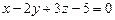 .
.
7. Что определяют в пространстве 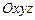 приведенные ниже равенства:
приведенные ниже равенства:
а) 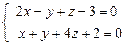 ; б)
; б)  ; в)
; в) 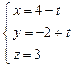 ?
?
Какую геометрическую информацию можно извлечь из приведенных равенств?
8. Найти параметрические уравнения прямой  , проходящей через точку
, проходящей через точку  перпендикулярно плоскости
перпендикулярно плоскости 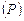 :
:  .
.
9. Найти канонические и параметрические уравнения прямой  , проходящей через точку
, проходящей через точку  параллельно прямой
параллельно прямой  :
:  .
.
10. Найти канонические уравнения прямой  , заданной как пересечение двух плоскостей
, заданной как пересечение двух плоскостей  :
:  и
и 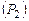 :
: 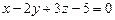 .
.
11. Найти точку пересечения прямой 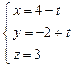 с плоскостью
с плоскостью  .
.
Домашнее задание.
1. Найти общее уравнение плоскости, проходящей через три точки  .
.
2. Найти канонические и параметрические уравнения прямой, являющейся пересечением плоскостей  .
.
3. Найти точку пересечения прямой, проходящей через точку  перпендикулярно плоскости
перпендикулярно плоскости  , с этой плоскостью.
, с этой плоскостью.
Фдз 11. Обзор основных задач занятий 2-10.
Проверка навыков решения основных задач по темам занятий 2-10.
1. Для матриц 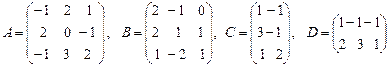 найти следующие произведения:
найти следующие произведения:  .
.
2. Вычислить определители матриц:  ,
, 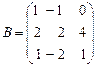 .
.
3. Разложением по 3-й строке вычислить определитель матрицы  .
.
4. Найти обратную матрицу для матрицы  .
.
5. Решить систему 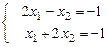 двумя способами:
двумя способами:
а) с помощью правила Крамера; б) с помощью обратной матрицы.
6. Решить методом Гаусса систему (или доказать несовместность): 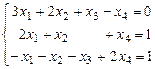 .
.
7. 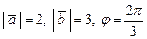 - угол между
- угол между 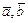 . Найти
. Найти 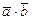 .
.
8.  . Найти
. Найти 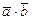 .
.
9.  . Найти
. Найти 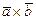 .
.
10.  . Найти
. Найти 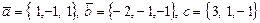 .
.
11. Найти каноническое уравнение прямой, проходящей через точки 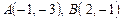 .
.
12. Найти общее уравнение плоскости, проходящей через три точки 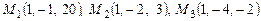 .
.
 2015-10-22
2015-10-22 311
311








