Компланарные, некомпланарные тройки векторов. Ориентация тройки векторов.
Векторное произведение: определение; свойства; координатное выражение.
Смешанное произведение: определение; свойства; координатное выражение. Условие компланарности тройки векторов.
1. Какие тройки векторов называются компланарными?
2. Дать определение правой (левой) тройки векторов.
3. Определить с помощью соответствующих рисунков ориентацию следующих троек векторов: 1) 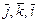 ; 2)
; 2) 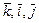 ; 3)
; 3) 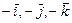 , где
, где 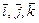 - орты осей
- орты осей 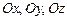 .
.
4. Дать определение векторного произведения 
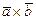 векторов
векторов 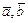 и сформулировать его свойства и геометрический смысл.
и сформулировать его свойства и геометрический смысл.
5. Записать формулу, по которой находится координатное выражение 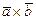 .
.
6. Вычислить 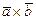 в следующих случаях:
в следующих случаях:
1) 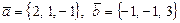 ; 2)
; 2) 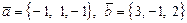 ;
;
3) 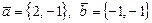 ; 4)
; 4) 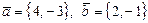 .
.
7. Найти площадь параллелограмма, построенного на векторах 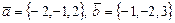 .
.
8. Найти площадь треугольника 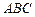 на плоскости
на плоскости 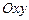 с вершинами в точках
с вершинами в точках 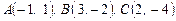 .
.
9. Найти координаты орта 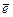 , перпендикулярного одновременно векторам
, перпендикулярного одновременно векторам 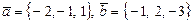 и такого, чтобы тройка
и такого, чтобы тройка 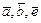 была правой.
была правой.
10. Дать определение смешанного произведения 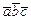 векторов
векторов 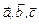 и указатьего геометрический смысл.
и указатьего геометрический смысл.
11. Вычислить 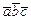 в случаях:
в случаях:
1) 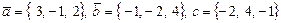 ; 2)
; 2) 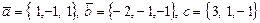 .
.
С помощью найденных результатов определите ориентацию этих троек векторов.
12. Найти объем пирамиды 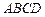 с вершинами
с вершинами 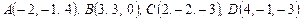 .
.
13. Выяснить, лежат ли точки 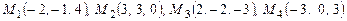
на одной плоскости.
________________________________________________________________________
Домашнее задание.
1. Найти координаты вектора 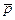 , удовлетворяющего следующим условиям:
, удовлетворяющего следующим условиям:
а) 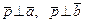 ; б)
; б) 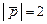 ; в)
; в) 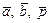 - левая тройка, если
- левая тройка, если  .
.
2. Вычислить площадь треугольника 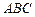 с вершинами
с вершинами 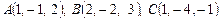 .
.
3. Найти объем пирамиды 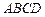 с вершинами
с вершинами 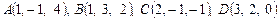 .
.
4. При каком значении параметра 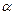 точки
точки 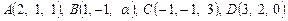 лежат в одной плоскости?
лежат в одной плоскости?
 2015-10-22
2015-10-22 295
295








