- это причинная модель статист. лин.связи м/у двумя колич-ными переменными х и у, предст-ная уравнением y = a + bx, где х – незав.переменная, y –зависимая.Коэф-т регрессии- b и свободный член ур-ния регрессии- a вычисляются по формулам:b = rxy Sy/Sx; a = y - bx,
Пусть  , кот.заданы своей выборкой
, кот.заданы своей выборкой  . Х=[х1,х2...хn] Y= [y1,y2..yn] (столбцы).
. Х=[х1,х2...хn] Y= [y1,y2..yn] (столбцы).
Будем рассм. парную связь в кот.:  все др.факторы приводят к некоторым отклонениям опытного зн-я от теорет.
все др.факторы приводят к некоторым отклонениям опытного зн-я от теорет. 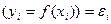 Будем отклонения называть- случ. теорет. отклонениями (ошиб.). В кач-ве ф-ции f(x) будем принимать ф-ю регрессии, те. ф-ю условное математ.ожидание: f(xi)= М(yi|xi). Чаще всего в кач-ве усл. матем.ожид.приним. линейную ф-ю: М(yi|xi)=а+bxi à yi= а+bxi +
Будем отклонения называть- случ. теорет. отклонениями (ошиб.). В кач-ве ф-ции f(x) будем принимать ф-ю регрессии, те. ф-ю условное математ.ожидание: f(xi)= М(yi|xi). Чаще всего в кач-ве усл. матем.ожид.приним. линейную ф-ю: М(yi|xi)=а+bxi à yi= а+bxi +  , где
, где  .
.  - для любой (.) (*)-лин.парная регрессия. Для построения (*) необход.по опытным данным найти коэф. а,b, где b- коэф.регрессии. Схема –кореляц.поле. На него можно нанести бесконечное мн-во прямых, каждый из кот.будет характеризовать а,b. Необходимо найти "наилучшую" прямую, т.е ту кот. в сумме имеет наименьшее отклонение. Метод нахожд. называется- "МНК".
- для любой (.) (*)-лин.парная регрессия. Для построения (*) необход.по опытным данным найти коэф. а,b, где b- коэф.регрессии. Схема –кореляц.поле. На него можно нанести бесконечное мн-во прямых, каждый из кот.будет характеризовать а,b. Необходимо найти "наилучшую" прямую, т.е ту кот. в сумме имеет наименьшее отклонение. Метод нахожд. называется- "МНК".
30.Анализ коэф.корелляции и детерминации.
После того как найдена ф-я регрессии производится оценка значимости как ур-я регрессии так и так коэф. Оценка значимости ур-я регрессии в целом производ.с помощью Fкр Фишера. Провести с помощью коэф. корелляции.- Коэф.корел. - показатель тесноты связи (лин.) м/у результативн. признаком и фактором. Согласно опред.корел.,он для генеральн.совокупности их двух случ.велечин  à из Т.вероятности:
à из Т.вероятности:  (*), но на практике – коэф. корел. опред. по выборке. – Выборочный коэф.-( приближ.зн-е) оценка коэф.корел.генер.совокупности. rxy-оценка выборки (*).
(*), но на практике – коэф. корел. опред. по выборке. – Выборочный коэф.-( приближ.зн-е) оценка коэф.корел.генер.совокупности. rxy-оценка выборки (*).  ;
;  . (-1< r <1) при b>0 0<r< 1, при b<0 -1<r< 0.
. (-1< r <1) при b>0 0<r< 1, при b<0 -1<r< 0.
- Коэф.детерминации -характериз.долю (разброс) дисперсии результатив. признака ^yi, кот.объясняется лин.регрессией.
М/у коэф.коррел.и детермин. для лин.ф-ии существ.связь.Можно показать: r = r2 xy (коэф.детермин.=коэф.корелл.в кв.)
 . Для Нелин. регрессии:- индекс коррел.Rxy; - индекс детерминации R2xy
. Для Нелин. регрессии:- индекс коррел.Rxy; - индекс детерминации R2xy

31.Дисперсионный анализ лин. регрессии.
Основной целью дисперсионного анализа является исследование значимости различия между средними.
Центральное место в дисп.анализе занимает разложение общей суммы кв.отклонений результирующего показателя у от его сред.зн-я у (с чертой) на две части: объясненную и остаточную.
 Результаты расчетов сводим в табл.
Результаты расчетов сводим в табл.
34.Оценка значимости линейной регрессии. Осущ-ся с помощью F-критерия Фишера,котор. сопоставляет факторную(объясненную) и остаточную дисперсии в расчете на одну степень свободы.Для вычисления F- критерия Фишера используется разложение общей суммы квадратов отклонений 
Сравнение 2-х сумм квадратов отклонения позвол.вып-ть оценку значимости ур-я рег-ии.Устан-м число степеней своб. для кажд. суммы квадратов отклонений При этом число степеней свободы-число единиц совокупности выборки и число определяемых констант.Для общей суммы  одно значение вычисл. через
одно значение вычисл. через 
 ,число степ. своб. =(n-1).Тогда
,число степ. своб. =(n-1).Тогда  -выборочная общая дисперсия.При опр-ии числа степ. своб. для факторной суммы квадратов
-выборочная общая дисперсия.При опр-ии числа степ. своб. для факторной суммы квадратов  исп-ся выраж.
исп-ся выраж.  , число b хар-ет степень свободы. Тогда для остат-й суммы квадр. число степ. своб. = n-2.Знач. дан. сумма имеет одну степ. своб. и тогда: =
, число b хар-ет степень свободы. Тогда для остат-й суммы квадр. число степ. своб. = n-2.Знач. дан. сумма имеет одну степ. своб. и тогда: = 
 ,
, 
Приведен. соотнош. дают возмож. исп-ть их для оценки стат. значим-ти ур-я рег-ии., кот. вкл. след. этапы: (для оцен. знач. выдвиг. след. гипотезы)
1)  ,кот. утвержд. что факторн. сумма на 1-ну степ. своб. = остат.; и выдвиг альтернатив. гипот.
,кот. утвержд. что факторн. сумма на 1-ну степ. своб. = остат.; и выдвиг альтернатив. гипот.  ,в кот. говор-ся что эти суммы не равны.2)В кач-ве критерия примен. стат-ка представл-я собой отнош-е:
,в кот. говор-ся что эти суммы не равны.2)В кач-ве критерия примен. стат-ка представл-я собой отнош-е:  Предполог. при справедлив. гип-зе
Предполог. при справедлив. гип-зе  отнош-е F распределено по закону ФЫишера (F распр-е) к1=1,к2=n-2; Fтабл (к1,к2)-закон Фишера(привод в табл);3)Выбирается Ур-нь знач-ти α,кот. обыч приним 0,05; 0,1.4)По табл. Фиш. нах-ся знач F по заданному уровню α; 5)Сравнив-ся таблич знач и вычисл-е знач. F-крит. Фиш. Если Fфакр<Fтабл, то вероят-ть
отнош-е F распределено по закону ФЫишера (F распр-е) к1=1,к2=n-2; Fтабл (к1,к2)-закон Фишера(привод в табл);3)Выбирается Ур-нь знач-ти α,кот. обыч приним 0,05; 0,1.4)По табл. Фиш. нах-ся знач F по заданному уровню α; 5)Сравнив-ся таблич знач и вычисл-е знач. F-крит. Фиш. Если Fфакр<Fтабл, то вероят-ть  выше заданного Ур-ня α.И она не м.б. отклонена без существенного риска соверш. неправ. выбор о наличии связи м/у результат-м показат. и фактором. В этом случае Ур. рег. след. полог. незначимым. В против. случ. нулевая гипот. отверг. и приним альтернатив., и счит. Ур. рег. качественным(Fфакр<Fтабл)
выше заданного Ур-ня α.И она не м.б. отклонена без существенного риска соверш. неправ. выбор о наличии связи м/у результат-м показат. и фактором. В этом случае Ур. рег. след. полог. незначимым. В против. случ. нулевая гипот. отверг. и приним альтернатив., и счит. Ур. рег. качественным(Fфакр<Fтабл)
35.Прогноз по линейн. ур. рег-ии. Точечный расчет результир-й переем-й  д.б. дополнен расчет. стандарт. ошибки
д.б. дополнен расчет. стандарт. ошибки  . Для вывода формулы определения вел. станд. ошиб. результир-й пер-й
. Для вывода формулы определения вел. станд. ошиб. результир-й пер-й  рассмотр. Ур-елин. рег.:
рассмотр. Ур-елин. рег.:  ,подставив в него знач. для коэф. а получим
,подставив в него знач. для коэф. а получим  ,
, 
Выбороч. диспер. (квадрат станд. ошибки)  результ. переем.
результ. переем.  завис. от ошиибки
завис. от ошиибки  и ошиб. коэф. рег. b, т.е.
и ошиб. коэф. рег. b, т.е. 
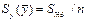
 -ошиб. коэф. рег.
-ошиб. коэф. рег.


получ. форм. для стандарт. ошиб. результир. переем-й  при зад-х знач-ях х хар-ет ошибку положения лин. рег.Вел станд-й ошибки будет мин-й при
при зад-х знач-ях х хар-ет ошибку положения лин. рег.Вел станд-й ошибки будет мин-й при 
По мере удалания от  Ош-ка возраст.. Т.е. чем > разность м/у
Ош-ка возраст.. Т.е. чем > разность м/у 
 тем > ош-ка.Поэт. след. иметь ввиду знач. результир. показ.След-т осущ-ть прогноз для х, кот. не слишком далеко расположены друг от друга.Фактич. знач. результир. фактора варьируется у вычисл-го
тем > ош-ка.Поэт. след. иметь ввиду знач. результир. показ.След-т осущ-ть прогноз для х, кот. не слишком далеко расположены друг от друга.Фактич. знач. результир. фактора варьируется у вычисл-го  .Индивид-е знач. м.б. отклон. от этого знач. на вел-ну, кот. опр-ся
.Индивид-е знач. м.б. отклон. от этого знач. на вел-ну, кот. опр-ся  и тогда формула буд. иметь вид:
и тогда формула буд. иметь вид: 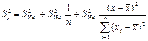


39.Индекс детерминации нелин. рег. Нелин. рег. хар-ся индексом корреляции  и детерминации
и детерминации  :
: 



Величина дан. показателя нах-ся в пределах 0<=  <=1, чем ближе она к 1, тем теснее связь, тем более надежное Ур-е рег.
<=1, чем ближе она к 1, тем теснее связь, тем более надежное Ур-е рег.
40,Индекс корреляц нелин.регрессии.
 (1-(Sост^2/Sу^2))^1/2
(1-(Sост^2/Sу^2))^1/2
Sост^2=  (yi-yxi)^2 / n
(yi-yxi)^2 / n
Sу^2 = 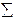 (yi-yср)^2 / n
(yi-yср)^2 / n
0<=Rxy<=1, чем ближе к 1, тем теснее связь между функцией и аргументом, тем более надежное уравнение регрессии.
41. Кривые Филипса - равносторонняя гипербола, характеризующая нелинейную зависимость междунормой безработици х и процентом прироста з/п у: у=а+b/х
42, Кривая Эйнгеля. Нем.статистик сформулир. В 1857г. закономерность, согласно кот. С ростом дохода доля его, расходуемая на непродовольственные товары, будет возрастать. Это увеличение имеет предел, поскольку сумма двух долей не может быть больше 100%, т.е. на отдельные непродовольств.товары этот предел может харак-ся величиной параметра а для уравнения вида: у=а-b/х.
43. Средняя ошибка аппроксим.
Кроме локальной характеристики аппроксимации результирующего показателя в эконометрике вводится глобальная характеристика качества аппроксимации, под которой понимается средняя ошибка аппрокс-ии. Если обозначить через Аi точечную(локальную)ошибку аппрокс.: Аi=|(yi-yxi)/yi|*100%, то интегральн.хар-ка аппрокс-ии А и средн.значен.будут вычисл.:
Аср.=( |(yi-yxi)/yi|*100%)*1/n = =1/n*
|(yi-yxi)/yi|*100%)*1/n = =1/n*  Аi.
Аi.
 2015-10-22
2015-10-22 547
547







