2015-10-22
5743
При параллельном переносе:
Момент инерции относительно какой-либо оси равен сумме момента инерции относительно центральной оси, параллельной данной, и произведения площади фигуры на квадрат расстояния между осями.
Для доказательства этой теоремы рассмотрим произвольную плоскую фигуру, площадь которой равна А, центр тяжести расположен в точке С, а центральный момент инерции относительно оси x будет Ix.
Вычислим момент инерции фигуры относительно некоторой оси x1, параллельной центральной оси и отстоящей от нее на расстоянии а (рис).
Ix1 = Σ y12 dA + Σ (y + a)2 dA =
= Σ y2 dA + 2a Σ y dA + a2 Σ dA.
Анализируя полученную формулу, отмечаем, что первое слагаемое - осевой момент инерции относительно центральной оси, второе слагаемое - статический момент площади этой фигуры относительно центральной оси (следовательно, он равен нулю), а третье слагаемое после интегрирования может быть представлено в виде произведения a2A, т. е. в результате получим формулу:
Ix1 = Ix + а2 А - теорема доказана.
|
|
|
На основании теоремы можно сделать вывод, что из ряда параллельных осей осевой момент инерции плоской фигуры будет наименьшим относительно центральной оси.
Относительно любой нецентральной оси, момент инерции больше, чем относительно параллельной её центральной.
При повороте:
Пусть известны моменты инерции произвольной фигуры (рис. 2. 6) относительно координатных осей Z,Y:
; 
; 
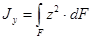(2.18)
Повернем оси z,y на угол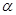 
против часовой стрелки, считая угол поворота осей в этом направлении положительным.
Найдем теперь моменты инерции сечения относительно повернутых осей 
, 
:
; 
; 
(2.19)
Координаты произвольной элементарной площадки в новой системе выражаются через координаты 
, 
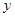прежней системы следующим образом:
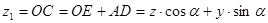(2.20)
(2.21)
Подставив эти выражения в (2.19) окончательно получим:
(2.22)
(2.23)
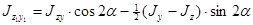(2.24)
Складывая почленно формулы (2.22),(2.23), находим
(2.25)
При повороте прямоугольных осей сумма моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.
При повороте координатных осей (рис. 1.3) моменты инерции сечения определяются по формулам:
,
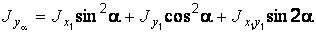, (1.11)
.
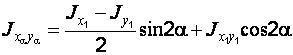Сумма осевых моментов инерции сечения относительно любой пары ортогональных осей с общим началом координат является постоянной величиной:
.
