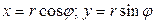
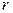 -полярный радиус
-полярный радиус
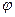 -полярный угол
-полярный угол


Считая 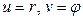 находим Якобиан
находим Якобиан
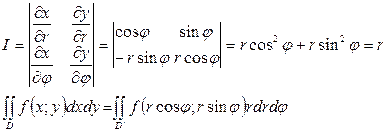
Вычисление двойного интеграла в полярной системе координат, так же как и в декартовой, сводится к последовательному интегрированию по переменным 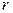 и
и 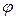 . Укажем правила расстановки пределов.
. Укажем правила расстановки пределов.
1. Пусть полюс не содержится внутри области интегрирования D, заключённой между лучами 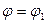 и
и 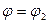 , и координатные линии
, и координатные линии 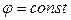 встречают её границу не более чем в двух точках или второй вид, также изображённый на рисунке.
встречают её границу не более чем в двух точках или второй вид, также изображённый на рисунке.
Полярные уравнения кривых ADC и ABC пусть будут 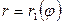 и
и 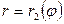 .
.
Интегрируя сначала по 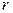 в пределах его изменения при постоянном
в пределах его изменения при постоянном 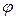 , т.е. от
, т.е. от 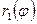 до
до 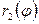 , а затем по
, а затем по 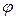 от
от 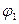 до
до 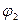 , получим
, получим
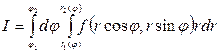
Интегрирование в обратном порядке, т.е. сначала по 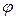 , а потом по
, а потом по 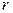 , обычно не встречается.
, обычно не встречается.
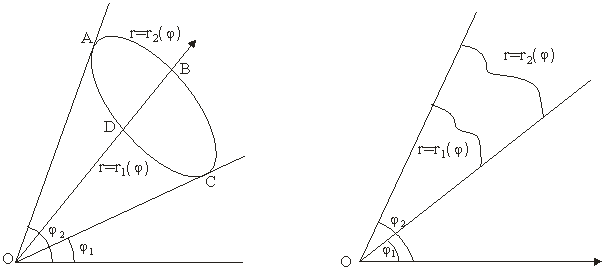
В частном случае, когда областью интегрирования служит часть кругового кольца 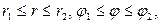 пределы интегрирования постоянны по обеим переменным:
пределы интегрирования постоянны по обеим переменным:
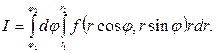
2. Пусть полюс содержится внутри области интегрирования и любой полярный адрес пересекает границу в одной точке (так называемая звёздная относительно полюса область). Интегрируя сначала по 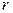 , а затем по
, а затем по 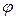 , получим
, получим
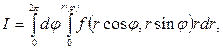
где 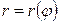 есть полярное уравнение границы области.
есть полярное уравнение границы области.
В частности, при 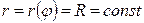 , т.е. когда область интегрирования есть круг с центром в полюсе, будем иметь,
, т.е. когда область интегрирования есть круг с центром в полюсе, будем иметь,
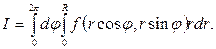
Пример:
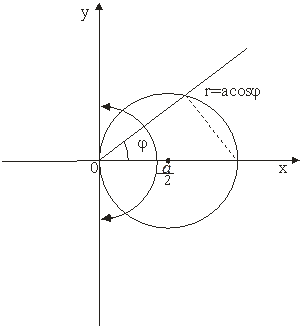
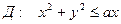
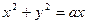
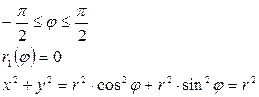
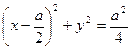
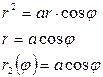
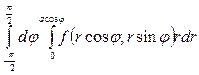
Приложение двойного интеграла в задачах геометрии и механики
1.Вычисление объема
Объем криволинейного цилиндра, ограниченного поверхностью 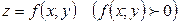 , снизу плоскостью
, снизу плоскостью 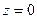 и с боковых сторон цилиндрической поверхностью, направляющая для которой граница области
и с боковых сторон цилиндрической поверхностью, направляющая для которой граница области 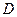 , а образующие параллельны оси
, а образующие параллельны оси 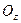 , равна двойному интегралу:
, равна двойному интегралу:
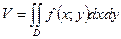
т.е. с помощью двойных интегралов можно вычислять объёмы тел.
Пример:
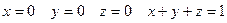
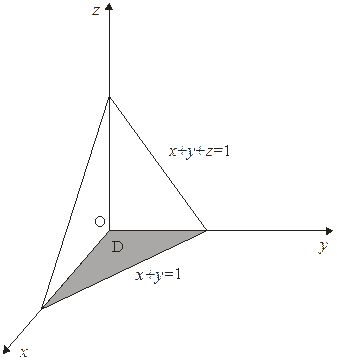
Имеем
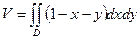
где D-треугольная область интегрирования, ограниченная прямыми 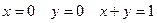
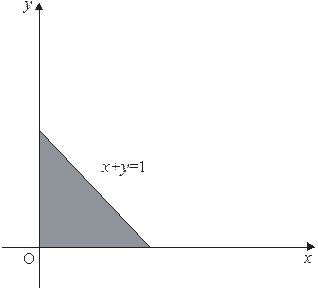
Расставляя пределы интегрирования в двойном интеграле, получаем
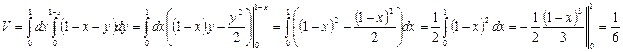
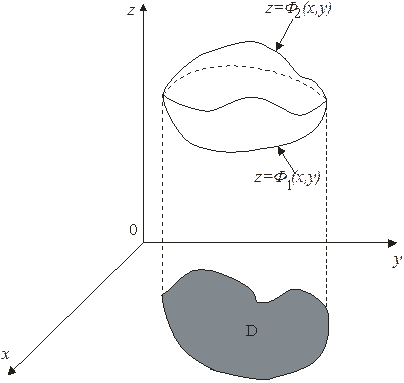
Если тело, объём которого ищется, ограничено сверху поверхностью 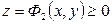 , а снизу поверхностью
, а снизу поверхностью 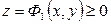 , причём проекцией обеих поверхностей на плоскость
, причём проекцией обеих поверхностей на плоскость  является область
является область 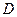
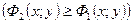 , то объем тела равен разности объемов двух цилиндрических тел: первого, ограниченного поверхностью
, то объем тела равен разности объемов двух цилиндрических тел: первого, ограниченного поверхностью 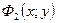 с основанием
с основанием 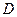 , второго
, второго 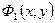 с тем же основанием.
с тем же основанием.
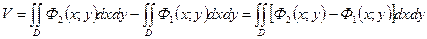
Формула верна не только тогда, когда 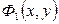 и
и 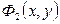 неотрицательны, но и тогда, когда
неотрицательны, но и тогда, когда 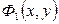 и
и 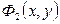 - любые непрерывные функции, удовлетворяющие соотношению
- любые непрерывные функции, удовлетворяющие соотношению 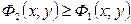 .
.
Если в области 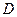 функция меняет знак, то разбиваем область
функция меняет знак, то разбиваем область 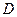 на две части:
на две части: 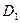 ,в которой
,в которой 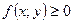 и
и 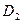 , где
, где 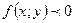 . Предположим, что существуют двойные интегралы по
. Предположим, что существуют двойные интегралы по 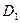 и
и 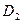 . Интеграл по области
. Интеграл по области 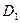 положителен и равен объему тела, расположенного над плоскостью
положителен и равен объему тела, расположенного над плоскостью 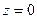 . Интеграл по области
. Интеграл по области 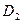 отрицателен и равен по абсолютной величине объему тела, расположенного под плоскостью
отрицателен и равен по абсолютной величине объему тела, расположенного под плоскостью 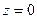 .Таким образом, интеграл по области
.Таким образом, интеграл по области 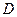 выражает разность соответствующих объемов.
выражает разность соответствующих объемов.
2.Вычисление площади плоской области
Площадь S области D может быть вычислена с помощью двойного интеграла по формуле
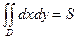
Эта формула более универсальна, чем соответствующая формула, выражающая площадь криволинейной трапеции с помощью определённого интеграла, так как она применима не только к криволинейным трапециям, но и к фигурам, расположенным произвольно по отношению к координатным осям.
Пример: Вычислить площадь области D, ограниченной линиями 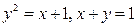 .
.
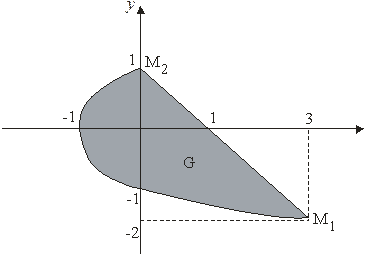
Область D представляет собой фигуру, ограниченную слева параболой 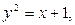 справа прямой
справа прямой 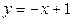 . Решая совместно уравнения параболы и прямой, находим точки их пересечения: M1(3;-2), M2(0;1). Следовательно, искомая площадь
. Решая совместно уравнения параболы и прямой, находим точки их пересечения: M1(3;-2), M2(0;1). Следовательно, искомая площадь
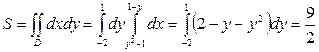
При вычислении двойных интегралов с помощью повторного интегрирования одним из главных моментов является расстановка пределов интегрирования. Поэтому полезно запомнить следующее правило: если все прямые, параллельные оси Oy, входят в область интегрирования D на линии, заданной одним уравнением, и выходят из области на линии, заданной одним уравнением, то внутренний интеграл целесообразно брать по переменной y, а внешний – по x; аналогично, если все прямые, параллельные оси Ox, входят в область интегрирования на линии, заданной одним уравнением (в данном случае на параболе), и выходят на линии, заданной одним уравнением (в данном случае на прямой), то внутренний интеграл следует брать по переменной x, а внешний – по y; в этом случае область интегрирования не нужно разбивать на части.
2.Вычисление площади поверхности
Площадь поверхности: 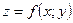 , где
, где 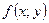 -непрерывна и имеет частные производные в области
-непрерывна и имеет частные производные в области 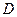 , в которую проектируется поверхность, может быть вычислена по формуле:
, в которую проектируется поверхность, может быть вычислена по формуле:
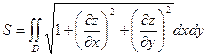
Если уравнение поверхности 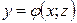 и выполняются аналогичные условия для функции
и выполняются аналогичные условия для функции 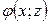 в области
в области 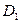 , то площадь поверхности
, то площадь поверхности
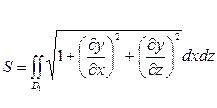
Если уравнение поверхности 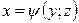 и выполнены условия для функции
и выполнены условия для функции 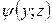 в области
в области 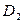 , то площадь поверхности
, то площадь поверхности
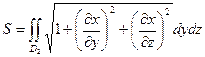
Пример:
Вычислить площадь поверхности сферы, если центр сферы в начале координат.
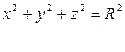
Уравнение верхней полусферы: 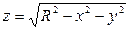 .
.
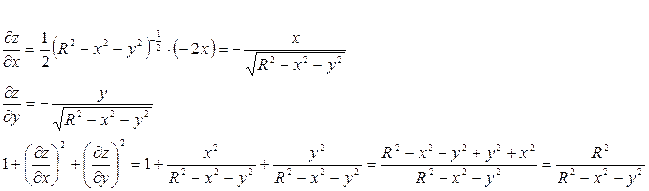
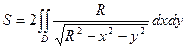
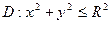
Границы: 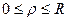 ,
, 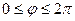
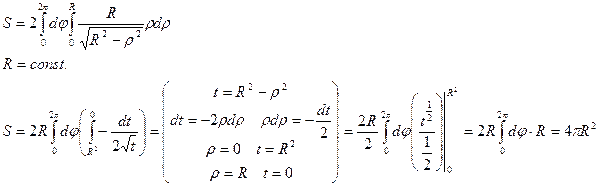
1.Вычисление массы пластинки
Плотность распределения вещества.
Пусть в области D распределено некоторое вещество, рассмотрим участок 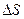 в этой области, масса этого участка
в этой области, масса этого участка 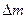
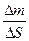 - средняя плотность
- средняя плотность
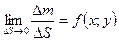
Этот предел называется поверхностной плотностью в точке и зависит от координат этой точки. Будем считать эту плотность известной.
Рассмотрим материальную пластинку, т.е. некоторую область D, по которой распределена масса m с плотностью 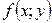 . Вычислим массу этой пластинки, считая, что
. Вычислим массу этой пластинки, считая, что 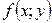 - непрерывная функция. Для этого разобьем область D на участки
- непрерывная функция. Для этого разобьем область D на участки 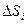 и возьмем по точке
и возьмем по точке 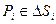
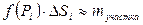
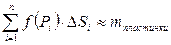
Общее значение массы пластинки:
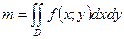
Пример: Определить массу квадратной пластинки со стороной 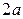 , если плотность
, если плотность 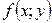 в каждой точке
в каждой точке 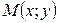 пропорциональна квадрату расстояния от точки M до точки пересечения диагоналей, и коэффициент пропорциональности равен k.
пропорциональна квадрату расстояния от точки M до точки пересечения диагоналей, и коэффициент пропорциональности равен k.
Решение: Выберем систему координат так, как показано на рисунке
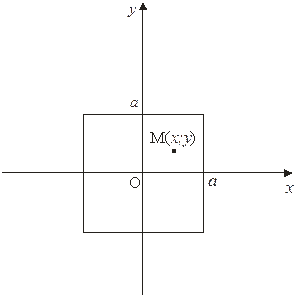
Пусть 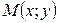 - произвольная точка квадратной пластинки. Тогда квадрат расстояния от точки M до точки пересечения диагоналей
- произвольная точка квадратной пластинки. Тогда квадрат расстояния от точки M до точки пересечения диагоналей 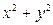 . Следовательно, плотность в точке M
. Следовательно, плотность в точке M
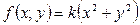
По формуле имеем
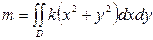
Учитывая, что подынтегральная функция чётна относительно x и y, а область интегрирования симметрична относительно осей координат, можно ограничиться вычислением интеграла по той части области D, которая расположена в I четверти, т.е.
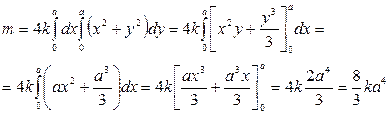
2.Момент инерции плоской фигуры
Моментом инерции материальной точки M, массы m, относительно некоторой точки O называется произведение массы на квадрат расстояния.
Пусть дана система материальных точек 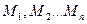 с массами
с массами 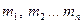 . Тогда момент инерции системы материальных точек находится по формуле:
. Тогда момент инерции системы материальных точек находится по формуле:
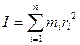
Рассмотрим плоскую фигуру D, которая располагается в плоскости Oxy, и найдем ее момент инерции относительно начала координат; будем считать поверхностную плотность равной единице. Разобьем эту фигуру на участки 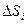 , на каждом участке возьмем точку
, на каждом участке возьмем точку 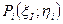 , и так как поверхностная плотность равна единице, масса площадки равна
, и так как поверхностная плотность равна единице, масса площадки равна 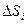 (ее площади). Назовём элементарным моментом инерции площадки
(ее площади). Назовём элементарным моментом инерции площадки 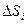 величину равную
величину равную 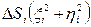 . Момент инерции всей фигуры D относительно начала координат или полярный момент инерции:
. Момент инерции всей фигуры D относительно начала координат или полярный момент инерции:
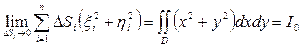
Интегралы
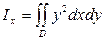
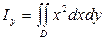
Называются соответственно моментами инерции фигуры D относительно осей Ox и Oy.
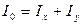
Отметим ещё, что интеграл 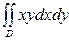 называется центробежным моментом инерции; он обозначается
называется центробежным моментом инерции; он обозначается 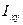 .
.
Пример:
Вычислить момент инерции круга радиуса R относительно его центра.
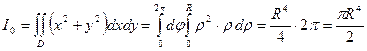
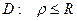
Если поверхностная плотность не равна единице, а является некоторой функцией 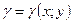
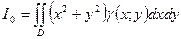
3.Координаты центра масс пластинки
Координаты центра масс системы материальных точек 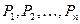 с массами
с массами 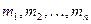 определяются по формулам:
определяются по формулам:
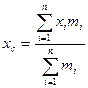
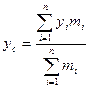
Будем считать поверхностную плотность равной единице. Определим координаты центра масс пластинки, занимающей область D. D разобьём на части 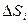 . Если поверхностная плотность равна единице, то масса площадки будет равна её площади. Если приближённо считать, что вся масса площадки
. Если поверхностная плотность равна единице, то масса площадки будет равна её площади. Если приближённо считать, что вся масса площадки 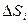 сосредоточена в какой-либо её точке
сосредоточена в какой-либо её точке 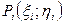 , то можно рассматривать пластинку как систему материальных точек. Тогда
, то можно рассматривать пластинку как систему материальных точек. Тогда
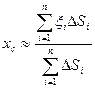
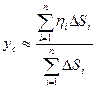
Перейдем к пределу, устремив 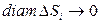
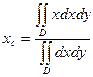
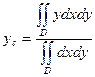
Если поверхностная плотность постоянна, то координаты центра масс находятся по тем же формулам.
Пусть поверхностная плотность 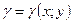 , тогда формулы для координат центра масс:
, тогда формулы для координат центра масс:
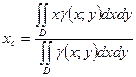
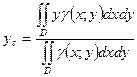
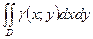 - величина массы рассматриваемой пластинки.
- величина массы рассматриваемой пластинки.
4.Статические моменты плоской фигуры
Статические моменты пластинкиотносительно осей Oy и Ox
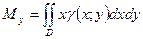
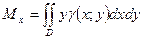
Пример: Найти координаты центра масс однородной пластинки, ограниченной двумя параболами 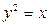 и
и 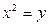 .
.
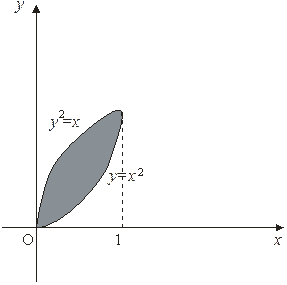
Сначала вычислим массу пластинки
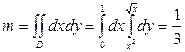
Далее вычислим статические моменты её относительно осей координат:
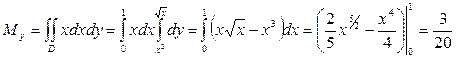
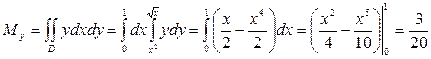
Затем формулам найдём координаты центра масс
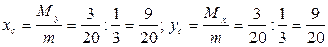
Итак, 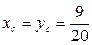 .
.
 2015-07-04
2015-07-04 9328
9328