Получим условия оптимальности, которым должна удовлетворять искомая управляющая последовательность. С этой целью интерпретируем сформулированную выше задачу как задачу математического программирования.
Представим критерий (4.2) как некоторую функцию искомого управления

Здесь под и и £ понимаются последовательности 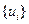 ,
,  , записанные для определенности в виде расширенных векторов
, записанные для определенности в виде расширенных векторов  с размерностями (N+l)m и (N+l)r соответственно. Зависимость функции конечного состояния J от и и
с размерностями (N+l)m и (N+l)r соответственно. Зависимость функции конечного состояния J от и и  неявная и проявляется через уравнение (4.1). Формально, задача оптимизации состоит в отыскании среди допустимых такого вектора и, который обращает в минимум критерий
неявная и проявляется через уравнение (4.1). Формально, задача оптимизации состоит в отыскании среди допустимых такого вектора и, который обращает в минимум критерий  . А это — обычная задача математического программирования. Необходимое условие оптимальности в такой задаче [28] сводится к выполнению условия неотрицательности производной
. А это — обычная задача математического программирования. Необходимое условие оптимальности в такой задаче [28] сводится к выполнению условия неотрицательности производной  в искомой точке и по любому допустимому направлению
в искомой точке и по любому допустимому направлению  , т. е.
, т. е.

Здесь и в дальнейшем запись 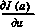 используется для обозначения градиента скалярной функции J(и) по векторному аргументу и, вычисленного в точке и = а. Под градиентом
используется для обозначения градиента скалярной функции J(и) по векторному аргументу и, вычисленного в точке и = а. Под градиентом  , как известно, понимается вектор (столбец), составленный из первых частных производных функции / по всем аргументам вектора и. В данном случае
, как известно, понимается вектор (столбец), составленный из первых частных производных функции / по всем аргументам вектора и. В данном случае  можно представить следующим образом:
можно представить следующим образом:

где через  в свою очередь обозначен градиент функции J по отдельному вектору
в свою очередь обозначен градиент функции J по отдельному вектору  .
.
Поясним теперь термин допустимое направление. Под допустимым направлением  понимается такой вектор, который, будучи добавленным к вектору и, не приведет к нарушению исходных ограничений по управлению ни при какой сколь угодно малой величине модуля самого вектора бы. Другими словами,
понимается такой вектор, который, будучи добавленным к вектору и, не приведет к нарушению исходных ограничений по управлению ни при какой сколь угодно малой величине модуля самого вектора бы. Другими словами,  считается допустимым, если выполняется условие
считается допустимым, если выполняется условие  , где под U пожимается совокупность всех допустимых множеств
, где под U пожимается совокупность всех допустимых множеств  , а
, а  является достаточно малым неотрицательным числом. Отметим также, что выписывая те или иные частные производные, будем, естественно, полагать, не оговаривая специально, что они существуют.
является достаточно малым неотрицательным числом. Отметим также, что выписывая те или иные частные производные, будем, естественно, полагать, не оговаривая специально, что они существуют.
С представленным здесь условием оптимальности работать трудно в виду того, что в нем используется расширенный вектор управления и, как правило, имеющий очень большую размерность. Преобразуем это условие к более простому виду. С этой целью среди множества допустимых векторов  рассмотрим лишь те, которые имеют ненулевые компоненты только в один единственный i -й момент. Другими словами, потребуем
рассмотрим лишь те, которые имеют ненулевые компоненты только в один единственный i -й момент. Другими словами, потребуем 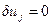 для всех
для всех 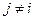 , а при
, а при 
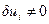 . Тогда условие оптимальности принимает более простой вид, а именно,
. Тогда условие оптимальности принимает более простой вид, а именно,

для всех допустимых  т. е. удовлетворяющих условию
т. е. удовлетворяющих условию
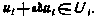
Так как соотношение (4.4) справедливо для любого момента 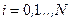 , товместо одного условия оптимальности получаем целую совокупность условий оптимальности вида (4.4). Преимущества этих условий заключаются в том, что в каждом из них участвует лишь один вектор управления
, товместо одного условия оптимальности получаем целую совокупность условий оптимальности вида (4.4). Преимущества этих условий заключаются в том, что в каждом из них участвует лишь один вектор управления  размерности т.
размерности т.
Физический смысл каждого из условий (4.4) заключается в том, что вариация терминального критерия (4.2) за счет вариации управления в i -й момент, вычисленная относительно оптимального управления, есть величина неотрицательная.
Условия оптимальности (4.4) в явном виде пока не связаны с исходной математической моделью. Установим эту связь. С этой целью раскроем производные  , связав последние с уравнением (4.1). Сначала покажем, каким образом может быть вычислена производная
, связав последние с уравнением (4.1). Сначала покажем, каким образом может быть вычислена производная 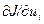 при любом управлении и и любом возмущении
при любом управлении и и любом возмущении  . Для этого продифференцируем функцию J = F(xN+l) по вектору
. Для этого продифференцируем функцию J = F(xN+l) по вектору  с учетом связи (4.1). Можно записать следующую цепочку соотношений:
с учетом связи (4.1). Можно записать следующую цепочку соотношений:


Здесь через  обозначены матрицы частных производных функции
обозначены матрицы частных производных функции  по своим аргументам
по своим аргументам  и
и  соответственно. Причем эти матрицы сформированы по следующему правилу: каждый столбец матрицы представляет собой градиент соответствующей компоненты вектор-функции по вектор-аргументу. Вводя формально обозначения
соответственно. Причем эти матрицы сформированы по следующему правилу: каждый столбец матрицы представляет собой градиент соответствующей компоненты вектор-функции по вектор-аргументу. Вводя формально обозначения

получаем более компактное выражение для производной
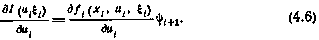
Введем теперь в рассмотрение также формально следующую скалярную функцию:

которая представляет собой по сути скалярное произведение вектора  , определяемого в соответствии с рекуррентным соотношением (4.5), и вектора
, определяемого в соответствии с рекуррентным соотношением (4.5), и вектора  , являющегося правой частью исходного уравнения (4.1). Функция Нi определяемая согласно (4.7), называется гамильтонианом. Подчеркнём, что в общем случае гамильтониан является случайной функцией, так как зависит от возмущения
, являющегося правой частью исходного уравнения (4.1). Функция Нi определяемая согласно (4.7), называется гамильтонианом. Подчеркнём, что в общем случае гамильтониан является случайной функцией, так как зависит от возмущения 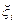 . Как увидим в дальнейшем, гамильтониан является удобной конструкцией при формировании как условий оптимальности, так и реализации различных численных методов оптимизации. Начнем с условий оптимальности. Нетрудно установить, что частные производные гамильтониана по своим аргументам имеют следующий вид:
. Как увидим в дальнейшем, гамильтониан является удобной конструкцией при формировании как условий оптимальности, так и реализации различных численных методов оптимизации. Начнем с условий оптимальности. Нетрудно установить, что частные производные гамильтониана по своим аргументам имеют следующий вид:

С учетом этого исходные уравнения движения (4.1), а также соотношения (4.5), определяющие вектор 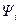 , могут быть приведены к следующей канонической форме:
, могут быть приведены к следующей канонической форме:
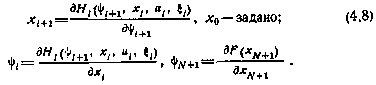
Уравнение для вектора 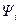 принято называть сопряженным по отношению к исходному уравнению для вектора
принято называть сопряженным по отношению к исходному уравнению для вектора  . Поэтому и сам вектор
. Поэтому и сам вектор 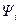 , удовлетворяющий системе (4.8), будем называть сопряженным вектором. Для его определения при известном управлении необходимо, как это следует из системы (4.8), определить сначала траекторию движения в прямом времени при заданном начальном условии. И только после этого в обратном времени найти сопряженный вектор с учетом найденной траектории и граничного условия, накладываемого на вектор
, удовлетворяющий системе (4.8), будем называть сопряженным вектором. Для его определения при известном управлении необходимо, как это следует из системы (4.8), определить сначала траекторию движения в прямом времени при заданном начальном условии. И только после этого в обратном времени найти сопряженный вектор с учетом найденной траектории и граничного условия, накладываемого на вектор  .Необходимо также иметь в виду, что в силу наличия случайного возмущения в правых частях уравнений системы (4.8) сопряженный вектор в общем случае также является случайным.
.Необходимо также иметь в виду, что в силу наличия случайного возмущения в правых частях уравнений системы (4.8) сопряженный вектор в общем случае также является случайным.
Если теперь вернуться к выражению (4.6), то с использованием понятия гамильтониана его можно записать в виде

Учитывая, что, как правило, операции дифференцирования и математического ожидания перестановочны, а, следовательно, имеет место равенство

необходимые условия оптимальности (4.4) окончательно представить в виде следующей системы неравенств:

которые должны выполняться для всех допустимых  .
.
Таким образом, необходимые условия оптимальности в задаче программирования управления системой (4.1) с целью достижения минимума критерия (4.2) заключаются в выполнении системы неравенств (4.10), которые должны быть раскрыты с учетом исходной системы уравнений (4.1) и сопряженной системы уравнений (4.5) или, что то же самое, системы (4.8).
В общем случае непосредственное использование этих условий для решения задачи программирования оптимального управления затруднительно. Это связано с неконструктивностью самих условий (4.10), которая проявляется в том, что трудно вообще использовать систему неравенств для отыскания оптимального решения. Трудности усугубляются, с одной стороны, наличием в этих неравенствах операции математического ожидания (статистического осреднения по всем случайным факторам) и, с другой стороны, необходимостью для каждой конкретной реализации решать краевую задачу для системы уравнений (4.1) и (4.5). Оптимальное управление при этом должно в каждой реализации привести к выполнению как краевого условия «слева» в начальный момент для системы (4.1), так и краевого условия «справа» в конечный момент для системы (4.5).
Следует еще раз подчеркнуть, что соотношение (4.6) справедливо для любого фиксированного (не обязательно оптимального) управления. Поэтому оно может быть успешно использовано при получении оптимального управления с помощью численных методов оптимизации, так как позволяет при фиксированном управлении с помощью одного просчета сначала по уравнению (4.1), а затем по уравнению (4.6) определить сразу все компоненты 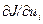 ,
,  вектора градиента
вектора градиента  в конкретной реализации. Использование соотношения (4.6) совместно с (4.1) и (4.5) для вычисления составляющих градиента в дальнейшем ради кратности будем называть методом сопряженных систем.
в конкретной реализации. Использование соотношения (4.6) совместно с (4.1) и (4.5) для вычисления составляющих градиента в дальнейшем ради кратности будем называть методом сопряженных систем.
Обсудим теперь наиболее распространенные частные случаи, когда необходимые условия оптимальности могут быть приведены к более конструктивной форме.
1. Ограничения на управление отсутствуют. В этом случае любые векторы  определяют допустимые направления, в том числе и векторы с одинаковыми модулями, но имеющие противоположные знаки. А это значит, что условия (4.10) могут быть выполнены лишь в виде строгих равенств
определяют допустимые направления, в том числе и векторы с одинаковыми модулями, но имеющие противоположные знаки. А это значит, что условия (4.10) могут быть выполнены лишь в виде строгих равенств
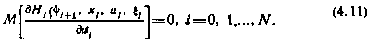
Следует отметить, что к этому случаю приходим также, когда ограничения на управления хотя и существуют, но выполняются автоматически.
Решение задачи программирования при этом сводится к использованию условия (4.11) на каждом шаге управления с целью выявления структуры управления и последующего решения системы (4.8) с найденной структурой.
2. Случайные возмущения отсутствуют,  ,
, 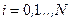 . Этот случай соответствует управлению детерминальной системой. Формально операция математического ожидания всюду опускается и необходимые условия оптимальности (4.40) принимают вид
. Этот случай соответствует управлению детерминальной системой. Формально операция математического ожидания всюду опускается и необходимые условия оптимальности (4.40) принимают вид

где гамильтониан  и векторы
и векторы 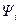 ,
,  являются детерминированными и определяются с помощью следующих соотношений:
являются детерминированными и определяются с помощью следующих соотношений:

Все трудности решения задачи с использованием условий оптимальности, обсуждаемые раньше при рассмотрении стохастической системы, сохраняются и здесь. Упрощение состоит лишь в том, что, как уже указывалось, операция математического ожидания отсутствует ввиду отсутствия самих случайных факторов.
3. Множество допустимых управлений  выпукло и гамильтониан
выпукло и гамильтониан 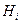 является выпуклой по
является выпуклой по  функцией. Прежде всего отметим, что каждое из условий (4.10) в общем случае может быть интерпретировано как необходимое условие минимума математического ожидания гамильтониана
функцией. Прежде всего отметим, что каждое из условий (4.10) в общем случае может быть интерпретировано как необходимое условие минимума математического ожидания гамильтониана  по вектору управления
по вектору управления  . Далее можно показать, что в случае выпуклости гамильтониана
. Далее можно показать, что в случае выпуклости гамильтониана 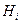 по
по  выпуклой будет и функция
выпуклой будет и функция  . А известно [31], что в случае выпуклости минимизируемой функции на выпуклом множестве минимум является единственным и поэтому необходимые условия оптимальности будут одновременно и достаточными. Учитывая это, каждое условие системы (4.10) в рассматриваемом случае оказывается эквивалентно условию достижения на оптимальном управлении математическим ожиданием гамильтониана
. А известно [31], что в случае выпуклости минимизируемой функции на выпуклом множестве минимум является единственным и поэтому необходимые условия оптимальности будут одновременно и достаточными. Учитывая это, каждое условие системы (4.10) в рассматриваемом случае оказывается эквивалентно условию достижения на оптимальном управлении математическим ожиданием гамильтониана  своего минимального по управлению значения. Иными словами, вместо (4.10) можно записать
своего минимального по управлению значения. Иными словами, вместо (4.10) можно записать

где через  , обозначено любое допустимое управление
, обозначено любое допустимое управление 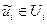 , a через
, a через  — искомое оптимальное управление.
— искомое оптимальное управление.
Естественно, возможны комбинации обсуждаемых частных случаев и соответственно условий оптимальности. Так, например, в детерминированном случае, т. е. при отсутствии возмущений
( ), и при выпуклости гамильтониана
), и при выпуклости гамильтониана 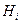 по
по  необходимые условия оптимальности принимают вид
необходимые условия оптимальности принимают вид

Заметим, что если при введении обозначений (4.6) вектор  определить как производную терминальной функции
определить как производную терминальной функции  по
по  с обратным знаком, т. е. в виде
с обратным знаком, т. е. в виде
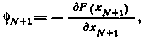
то в силу изменения знака у вектора 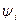 в условиях оптимальности (4.10) знак неравенства изменяется также на противоположный, и, как следствие, в условиях оптимальности (4.12), (4.13) операция минимума заменяется на операцию максимума. В детерминированном случае вместо (4.13) будем иметь
в условиях оптимальности (4.10) знак неравенства изменяется также на противоположный, и, как следствие, в условиях оптимальности (4.12), (4.13) операция минимума заменяется на операцию максимума. В детерминированном случае вместо (4.13) будем иметь
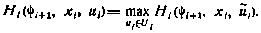
Последнее условие оптимальности в литературе обычно именуется как принцип максимума i[31] для детерминированных дискретных систем управления или кратко — как дискретный детерминированный принцип максимума. По аналогии условие (4.13) можно назвать дискретным детерминированным принципом минимума, а условие оптимальности (4.12)—дискретным стохастическим принципом минимума.
Согласно дискретному стохастическому принципу минимума (4.12) оптимальная программа управления дискретной системой (4.1) при условиях выпуклости 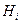 по
по  обеспечивает минимум математического ожидания гамильтониана на каждом шаге управления. Б дальнейшем увидим, что принцип минимума (максимума) для задач с непрерывным временем справедлив вне предположений о выпуклости гамильтониана. Однако для дискретных задач эти предположения оказываются существенными.
обеспечивает минимум математического ожидания гамильтониана на каждом шаге управления. Б дальнейшем увидим, что принцип минимума (максимума) для задач с непрерывным временем справедлив вне предположений о выпуклости гамильтониана. Однако для дискретных задач эти предположения оказываются существенными.
Покажем теперь, что в задаче управления дискретной системой (4.1) с целью минимизации интегротерминального критерия (4.3)

полученные условия оптимальности (4.10) или соответственно (4.11), (4.12) сохраняются. Однако вместо соотношений (4.7) и (4.5), определяющих гамильтониан 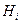 и сопряженный вектор
и сопряженный вектор 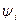 , теперь следует использовать следующие соотношения:
, теперь следует использовать следующие соотношения:
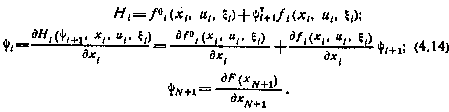
Чтобы убедиться в справедливости сказанного, введем, как уже упоминалось, дополнительную переменную  , определяемую согласно уравнению
, определяемую согласно уравнению  , сводя тем
, сводя тем
самым критерий (4.3) к виду (4.2)  .
.
Составим для полученной вновь задачи согласно (4.7) гамильтониан, обозначив его через 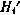 :
:

Условие оптимальности для этой задачи имеет вид (4.10) с учетом (4.8) при гамильтониане 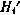 . Согласно (4.8) компонента
. Согласно (4.8) компонента  и вектор
и вектор 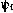 удовлетворяют следующим уравнениям:
удовлетворяют следующим уравнениям:


Так как  для всех
для всех 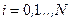 , то гамильтониан
, то гамильтониан  с точностью до составляющей
с точностью до составляющей  совпадает с гамильтонианом
совпадает с гамильтонианом 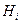 в (4.14). Поэтому выражению для производной
в (4.14). Поэтому выражению для производной  , участвующей в условиях оптимальности, можно придать прежний вид (4.9):
, участвующей в условиях оптимальности, можно придать прежний вид (4.9):
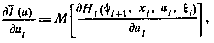
несмотря на то, что гамильтониан 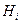 теперь определяется согласно (4.14) вместо (4.7). А это и означает, что условия оптимальности по форме останутся неизменными.
теперь определяется согласно (4.14) вместо (4.7). А это и означает, что условия оптимальности по форме останутся неизменными.
 2015-10-22
2015-10-22 1205
1205