Основные формулы интегрирования

1. =		2. =
3. =		4. =
5. =		6. =
7. =		8. =
9. =		10. =
11. =		12. =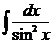
13. =		14. =
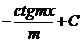
15. =		16. =
17. =		18. =
19. =		20. =
21. =		22. =

- «Определённый интеграл» необходимо использовать понятие определенного интеграла, формулу Ньютона-Лейбница для его вычисления, свойства определенного интеграла и методы интегрирования, а также использовать формулы интегрирования (см. выше).

- «Площадь криволинейной трапеции» необходимо использовать понятие определенного интеграла, формулу Ньютона-Лейбница для его вычисления, свойства определенного интеграла, а также использовать формулы интегрирования (см. выше), так же следует применять понятие определенного интеграла и его применение при вычислении площади криволинейной трапеции, учитывая случаи расположения фигуры в системе координат;

- «Геометрия» следует применять свойства геометрических фигур и тел, формулы вычисления площадей и объёмов геометрических фигур и тел.

Контрольная работа

Требования к оформлению контрольной работы

Контрольную работу следует выполнять в ученических тетрадях (желательно в клеточку). На обложке необходимо указать: название учебного заведения, название специальности, курс, номер группы, фамилию, имя, отчество и личный номер студента (который определяется по номеру в журнале группы). Условия задач переписывать не обязательно, достаточно указать номер задачи.

Повторение

Уравнения

Решить уравнения:

Вариант №1.	Вариант №2.	Вариант №3.
Вариант №4.	Вариант №5.	Вариант №6.
Вариант №7.	Вариант №8.	Вариант №9.
Вариант №10.	Вариант №11.	Вариант №12.

Неравенства

Решить неравенства:

Вариант №1.	Вариант №2.	Вариант №3.
Вариант №4.	Вариант №5.	Вариант №6.
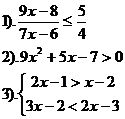
Вариант №7.	Вариант №8.	Вариант №9.
Вариант №10.	Вариант №11.	Вариант №12.

Теория пределов

Пределы

Вычислить:

Вариант №1.	Вариант №2.	Вариант №3.
Вариант №4.	Вариант №5.	Вариант №6.
Вариант №7.	Вариант №8.	Вариант №9.
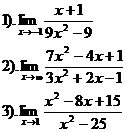
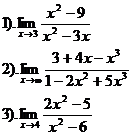
Вариант №10.	Вариант №11.	Вариант №12.