Пример1. Даны матрицы  , числа
, числа  и
и  .
.
Вычислить: 1)  ; 2)
; 2) 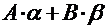 ; 3)
; 3)  ; 4)
; 4)  , если
, если
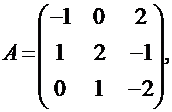
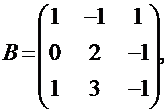


Решение. 1) Убеждаемся в том, что произведение матриц  и
и  определено. Действительно, так как указанные матрицы квадратные одного порядка, то произведение
определено. Действительно, так как указанные матрицы квадратные одного порядка, то произведение  и
и  существует. Найдем это произведение:
существует. Найдем это произведение:
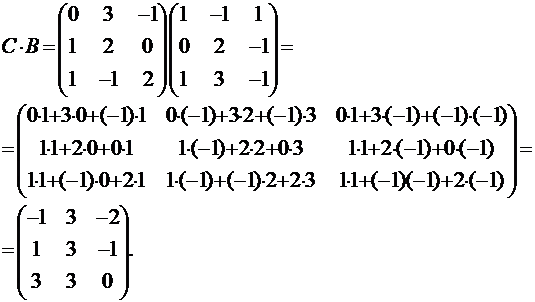
2) Вычислим линейную комбинацию матриц  . Воспользуемся правилом умножения матрицы на число и правилом вычитания матриц:
. Воспользуемся правилом умножения матрицы на число и правилом вычитания матриц:

3) Найдем матрицу выражения  . Для этого определим матрицу каждого слагаемого, используя определение степени матрицы:
. Для этого определим матрицу каждого слагаемого, используя определение степени матрицы:



4) Убеждаемся в том, что для матрицы  существует обратная матрица. Для этого вычислим определитель
существует обратная матрица. Для этого вычислим определитель
 .
.
Обратная матрица  существует, так как
существует, так как  . Её находим методом присоединенной матрицы. Для этого определяем алгебраические дополнения соответствующих элементов матрицы:
. Её находим методом присоединенной матрицы. Для этого определяем алгебраические дополнения соответствующих элементов матрицы:



Матрица  , присоединенная к матрице
, присоединенная к матрице  , имеет вид
, имеет вид

Обратную матрицу находим по формуле  , согласно которой
, согласно которой
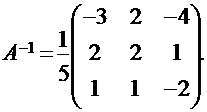
Убеждаемся в правильности нахождения обратной матрицы. Для этого проверяем равенство  . Действительно,
. Действительно,


Методы решения систем линейных алгебраических уравнений
 2017-11-30
2017-11-30 462
462








