2017-11-30
454
Пример. Даны координаты вершины пирамиды 
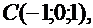
Найти: а) угол между векторами 
и 
;
б) площадь треугольника 
;
в) объем пирамиды 
.
а) Найти 
и 
, где 
, 
.
Решение. Найдем координаты векторов 
и 
:
,.
Найдем модули полученных векторов и их скалярное произведение:
, 
,
.
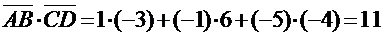
Определяем косинус угла между векторами: 
б) Вычислить площадь 
Площадь треугольника найдем, исходя из геометрического свойства векторного произведения: 
.
Найдем векторное произведение:
= 
.
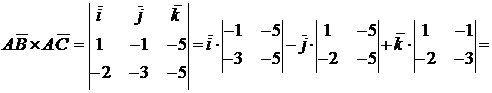
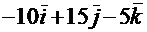Тогда 
.
в) Найти объём пирамиды .
Решение. Объём пирамиды найдем, исходя из геометрического свойства смешанного произведения:
