Определенный интеграл и его приложения

Теорема. Если y=f(x)- непрерывная функция, а F(x) - любая ее первообраз-

ная, то 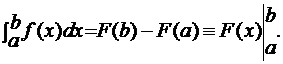(7)

Таким образом, чтобы вычислить определенный интеграл, нужно найти ее первообразную функцию F(x), т.е. взять неопределенный интеграл 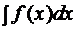, а затем вычислить разность 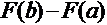. Напомним, что формула (7) называется формулой Ньютона-Лейбница.

Задача 14. Вычислить определенный интеграл .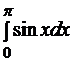

Решение. Применим формулу Ньютона-Лейбница:

 

 

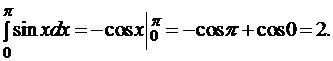
Вычисление площадей фигур. В декартовой системе координат

элементарной фигурой является криволинейная трапеция (рис.7), площадь которой вычисляется по формуле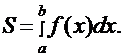

 

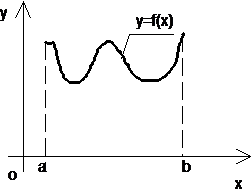
Рис.7

 

Задача. Найти площадь фигуры, ограниченной линиями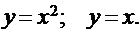

Решение: Построим чертеж к задаче (рис. 8). Из чертежа ясно, что

.

 

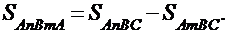Найдем координаты точки В. Для этого совместно решим уравнения

линий, точкой пересечения которых она явля­­ет­ся:

 

 

 

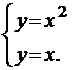
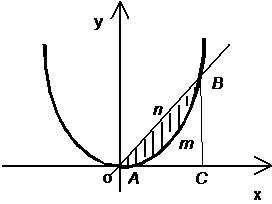Отсюда

Но тогда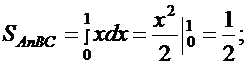

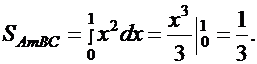
Окончательно находим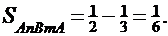

Рис.8

 

Титульный лист к контрольной работе.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Институт технологий (филиал) федерального государственного бюджетного образовательного учреждения высшего образования

«Донской государственный технический университет»