1. 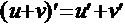 2.
2. 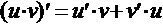 , в частности,
, в частности, 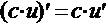 3.
3. 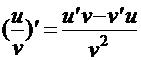 , где
, где 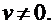
Задача. Найти производные следующих функций:
а) 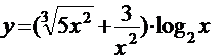 ; б)
; б) 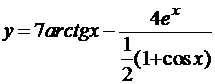 .
.
Решение. а) Преобразуем выражение в скобках, переходя к дробным и отрицательным показателям. Получим
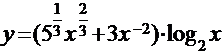 .
.
Используя правило дифференцирования произведения и суммы находим 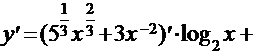
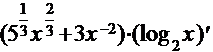 =
=
= 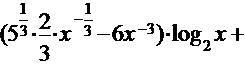
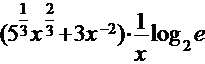 .
.
б) Проведем предварительное преобразование функции:
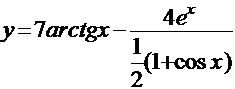 =
= 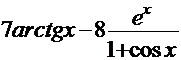 .
.
Используя правила дифференцирования произведения, суммы и частного, получим
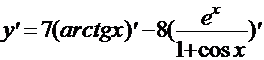 =
=
= 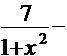
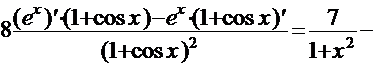
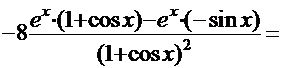
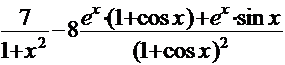 .
.
НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Неопределенным интегралом 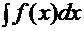 называется выражение
называется выражение 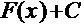 , где
, где 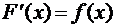 , а
, а 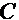 - произвольная константа, т.е.
- произвольная константа, т.е.
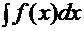 =
= 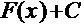 .
.
Замена переменных в неопределенном интеграле
Одним из основных методов интегрирования является метод замены переменных. Пусть требуется найти интеграл с непрерывной подынтегральной функцией
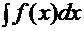 . (1)
. (1)
Сделаем замену переменных, положив
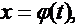 (2)
(2)
где функция 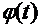 удовлетворяет следующим двум условиям:
удовлетворяет следующим двум условиям:
1) 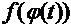 - непрерывная функция;
- непрерывная функция;
2) 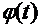 - непрерывно дифференцируемая функция, имеющая обратную функцию, тогда
- непрерывно дифференцируемая функция, имеющая обратную функцию, тогда 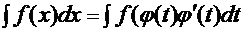 .
.
Задача 1. Найти неопределенный интеграл 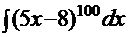 .
.
Решение: Положим, 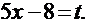 Дифференцируя это равенство, получим:
Дифференцируя это равенство, получим: 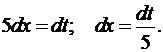
Но тогда 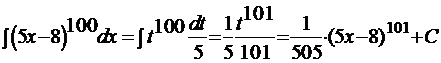 .
.
Задача 2. Найти неопределенный интеграл 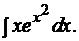
РHHешение: оложим 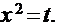 Такая замена очень естественна, так как, учитывая, что
Такая замена очень естественна, так как, учитывая, что 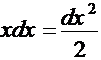 , наш интеграл можно записать в следующем порядке:
, наш интеграл можно записать в следующем порядке:
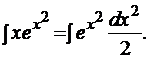 Итак,
Итак, 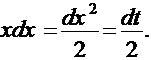
Тогда 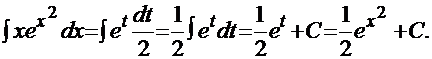
 2017-11-30
2017-11-30 292
292








