Медведева Н.С., Моисеева Ю.А., Степанов А.Г., Усикова И.В.
СИСТЕМЫ ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЯ
Оптимальные методы и теория принятия решений
Учебно – методическое пособие
Санкт-Петербург
УДК 681.3.06(075)
ББК 32.79
С
Системы поддержки принятия решения. Оптимальные методы и теория принятия решений: учеб.-метод. пособие/ Медведева Н.С., Моисеева Ю. А., Степанов А.Г., Усикова И.В.; ГУАП. ‑СПб., 2007. ‑00 с.
В учебно-методическом пособии рассматривается основные положения теории принятия решений и цикл лабораторных работ по дисциплине «Системы поддержки принятия решения» в части оптимальных методов и теории принятия решений. Излагается методика выполнения лабораторных работ и приводятся необходимые рекомендации. Учебно-методическое пособие предназначено для студентов, обучающихся по специальностям «Прикладная информатика в экономике», «Информационный сервис» и может быть использовано в составе дисциплины «Разработка управленческого решения» при подготовке по экономическим специальностям, для которых требуется изучение теории принятия решений.
Рецензент: профессор Международного банковского института доктор технических наук Кричевский М.Л.
© Н.С. Медведева 2008
© Ю.А. Моисеева 2008
© А.Г. Степанов 2008
© И.В. Усикова 2008
Содержание
Введение.. 6
1. Оптимальные методы... 8
1.1. Методы поиска экстремумов функций.. 8
1.2. Учет ограничений на значения переменных. 11
1.3. Использование Excel для поиска экстремумов функций.. 15
Лабораторная работа №1. Методы поиска экстремумов с помощью надстройки Поиск решения пакета Excel 24
2. Теория принятия решений.. 30
2.1. Основные понятия теории принятия решений.. 30
2.2. Математическая классификация задач разработки управленческого решения. 33
2.3. Однокритериальная статическая задача разработки управленческого решения в условиях определенности 36
Лабораторная работа №2. Решение однокритериальной статической задачи в условиях определенности. 41
2.4. Однокритериальная статическая задача разработки управленческого решения в условиях риска. 43
Метод сведения задачи в условиях риска к детерминированной. 45
Лабораторная работа №3. Решение однокритериальной статической задачи в условиях риска методом сведения стохастической задачи к детерминированной. 46
Методы оптимизации в среднем.. 48
Алгоритмический метод решения задачи в условиях риска. 51
Лабораторная работа №4. Решение однокритериальной статической задачи в условиях риска алгоритмическим методом 52
Метод Монте-Карло при решении задачи в условиях риска. 53
Лабораторная работа №5. Решение однокритериальной статической задачи в условиях риска методом Монте-Карло 56
Задачи в условиях риска с несколькими стохастическими параметрами. 58
2.5. Однокритериальная статическая задача в условиях неопределенности.. 58
Игры с противником. 61
Лабораторная работа №6. Решение однокритериальной статической задачи в условиях неопределенности при играх с противником.. 65
Игры с природой. 68
Лабораторная работа №7. Решение однокритериальной статической задачи в условиях неопределенности при играх с природой. 70
Игры с природой с экспериментами. 72
Лабораторная работа №8. Решение однокритериальной статической задачи в условиях неопределенности при играх с природой с экспериментами. 76
2.6. Многокритериальные задачи.. 78
Лабораторная работа №9. Решение многокритериальной задачи. 82
2.7. Динамические задачи разработки управленческого решения. 85
Общая постановка динамической задачи разработки управленческого решения. 85
Метод сетевого планирования. 87
Методы теории массового обслуживания. 89
Метод динамического программирования. 90
Задача управления запасами. 93
Методы вариационного исчисления и теории оптимального управления. 96
Метод сведения дискретной динамической задачи к статической. 97
Лабораторная работа №10. Решение дискретной задачи разработки управленческого решения методом сведения динамической задачи к статической. 98
2.8. Рациональные решения. 101
Общий алгоритм разработки управленческого решения. 101
Нереализуемые оптимальные решения. 103
Разработка альтернатив для принятия рациональных решений. 103
2.9. Экспертные методы.. 106
Определение круга экспертов. 106
Задачи, решаемые при проведении экспертизы.. 109
Разработка анкеты.. 110
Разработка методов обработки результатов. 111
Проведение анкетирования, обработка и выдача результатов и принятие решения. 112
Литература. 113
Приложение А. Пример титульного листа отчета о выполнении лабораторной работы. 115
Приложение Б. Содержание отчетов о выполнении лабораторных работ 116
Пример содержания отчета по лабораторной работе №2 «Решение однокритериальной статической задачи в условиях определенности». 116
Пример содержания отчета по лабораторной работе №3 «Решение однокритериальной статической задачи в условиях риска методом сведения стохастической задачи к детерминированной». 122
Пример содержания отчета по лабораторной работе №4 «Решение однокритериальной статической задачи в условиях риска алгоритмическим методом». 124
Пример содержания отчета по лабораторной работе №5 «Решение однокритериальной статической задачи в условиях риска методом Монте-Карло». 126
Пример содержания отчета по лабораторной работе №6 «Решение однокритериальной статической задачи в условиях неопределенности при играх с противником». 131
Пример содержания отчета по лабораторной работе №7 «Решение однокритериальной статической задачи в условиях неопределенности при играх с природой». 134
Пример содержания отчета по лабораторной работе №8 «Решение однокритериальной статической задачи в условиях неопределенности при играх с природой с экспериментами». 136
Пример содержания отчета по лабораторной работе №9 «Решение многокритериальной задачи». 138
Пример содержания отчета по лабораторной работе №10 «Решение дискретной задачи разработки управленческого решения методом сведения динамической задачи к статической». 143
Предметный указатель. 149
Введение
Системы поддержки принятия решения представляют собой класс информационных систем, предназначенных для решения управленческих задач. Работа таких систем позволяет автоматизировать процесс разработки управленческого решения за счет компьютерного поиска наилучшего варианта решения, подбора необходимой информации, формализации уже имеющихся знаний в предметной области и их использования в своих целях, решения задач измерения, ранжирования и классификации. На сегодняшний день отсутствует единый подход к классификации подобных систем. В основе настоящей работы лежит один из возможных вариантов такой классификации, представленный на рис. 1. В ее основе лежит разделение имеющихся знаний в рассматриваемой области на теоретические и прикладные. Во многом такое деление оказывается условным, поскольку развитие методов решения прикладных задач неизбежно приводит и к развитию теоретической их составляющей. С другой стороны, потребности практики обучения требуют систематизации уже имеющихся знаний и использования их в практических задачах. Поэтому в учебно-методическом пособии используется сочетание теоретической и практической составляющих используемой классификации в рамках единой рубрикации.
Настоящее учебно-методическое пособие содержит только часть материала, имеющего непосредственное отношение к системам поддержки принятия решения, а именно оптимальные методы и теорию принятия решения. Остальные составляющие структуры рис. 1 будут описаны в последующих публикациях.

Рис. 1. Используемая классификация систем поддержки принятия решения
Оптимальные методы
Методы поиска экстремумов функций
Экстремумомфункции  на интервале
на интервале  называется наибольшее или наименьшее значение функции относительно некоторой окрестности. Это значение может отличаться от наибольшего или наименьшего значения на всей области определения. Найти экстремум
называется наибольшее или наименьшее значение функции относительно некоторой окрестности. Это значение может отличаться от наибольшего или наименьшего значения на всей области определения. Найти экстремум  – это значит найти такое значение аргумента
– это значит найти такое значение аргумента  , при котором функция имеет максимум или минимум (рис. 2).
, при котором функция имеет максимум или минимум (рис. 2).

Рис. 2. Экстремум функции на интервале определения
Традиционным методом поиска экстремума является дифференциальное исчисление(метод И. Ньютона). Необходимым условием существования экстремума дифференцируемой на интервале функции является равенство нулю первой ее производной. Соответствующая точка рассматривается как критическая. Достаточным условием существования максимума дифференцируемой на интервале функции является отрицательное значение второй производной функции в критической точке, а минимума - положительное значение второй производной. Если вторая производная в рассматриваемой точке равна нулю, то экстремум не существует, а критическая точка является точкой перегиба.
Предположим, что функция изменяет свое значение на интервале определения  , но имеет экстремум вне интервала. Тогда возникает задача поиска находящихся как раз на границах интервала максимального и минимального значения функции (рис. 3). Отметим, что первая производная функции на границах интервала определения в этом случае вовсе не обращается в нуль. Поэтому использование традиционного метода поиска экстремума (метода И. Ньютона) в данном случае оказывается невозможным.
, но имеет экстремум вне интервала. Тогда возникает задача поиска находящихся как раз на границах интервала максимального и минимального значения функции (рис. 3). Отметим, что первая производная функции на границах интервала определения в этом случае вовсе не обращается в нуль. Поэтому использование традиционного метода поиска экстремума (метода И. Ньютона) в данном случае оказывается невозможным.

Рис. 3. Экстремум на границе интервала определения
Функция нескольких переменных  также может быть дифференцируема в некой точке (полный дифференциал). Если функция дифференцируема в некой точке, то существуют частные производные по каждой из переменных, причем в критической точке они обращаются в нуль
также может быть дифференцируема в некой точке (полный дифференциал). Если функция дифференцируема в некой точке, то существуют частные производные по каждой из переменных, причем в критической точке они обращаются в нуль 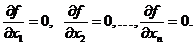 (обратное не верно). В зависимости от конкретного вида функции
(обратное не верно). В зависимости от конкретного вида функции  таких точек может быть ни одной, одна или несколько. Существование критической точки является необходимым, но не достаточным условием экстремума. Для его нахождения необходимо вычислить вторые чистые и смешанные производные критериальной функции
таких точек может быть ни одной, одна или несколько. Существование критической точки является необходимым, но не достаточным условием экстремума. Для его нахождения необходимо вычислить вторые чистые и смешанные производные критериальной функции

Производная в некой точке по направлению может рассматриваться как производная сечения многомерной функции плоскостью, образованной направлением и точкой. Вектор производных функции по каждой из координат в некой точке называется градиентом функции в заданной точке, а сам метод поиска экстремумов градиентным.
Достаточное условие существования локального экстремума формулируется следующим образом [15]: пусть функция  имеет критическую точку (
имеет критическую точку ( ), определяемую за счет вычисления выражений
), определяемую за счет вычисления выражений
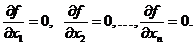
Тогда, если дифференциал второго порядка

больше нуля, то функция 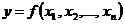 имеет минимум, а если меньше нуля, то функция
имеет минимум, а если меньше нуля, то функция 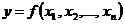 имеет максимум при любых
имеет максимум при любых  и
и  , не обращающихся в нуль одновременно. Если в зависимости от
, не обращающихся в нуль одновременно. Если в зависимости от  и
и  значение дифференциала может принимать и положительные, и отрицательные значения, то экстремума в критической точке нет.
значение дифференциала может принимать и положительные, и отрицательные значения, то экстремума в критической точке нет.
Если функция 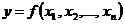 имеет несколько экстремумов, то их обычно называют локальными. Наибольший их локальных максимумов или наименьший из локальных минимумов называют глобальным.
имеет несколько экстремумов, то их обычно называют локальными. Наибольший их локальных максимумов или наименьший из локальных минимумов называют глобальным.
В качестве примера рассмотрим функцию двух переменных  . Приравняем к нулю ее первые частные производные
. Приравняем к нулю ее первые частные производные
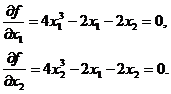
Вычитая из первого уравнения второе, имеем  , откуда
, откуда  . Подставляя
. Подставляя  в выражения для частных производных, имеем
в выражения для частных производных, имеем  . Получившееся уравнение имеет три решения: 0, 1, -1. Тогда критическими точками являются
. Получившееся уравнение имеет три решения: 0, 1, -1. Тогда критическими точками являются 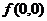 ,
,  и
и  .
.
Вторые частные производные имеет вид

Следуя [6], «разумным» образом выберем комбинацию приращений  и
и  равными +1 и –1, поскольку такие значения соответствуют максимально возможному диапазону изменения аргументов при переходе от одной критической точки к другой. Результаты вычислений вторых частных производных и дифференциала второго порядка при различных комбинациях
равными +1 и –1, поскольку такие значения соответствуют максимально возможному диапазону изменения аргументов при переходе от одной критической точки к другой. Результаты вычислений вторых частных производных и дифференциала второго порядка при различных комбинациях  и
и  сведены в таблицу 1.
сведены в таблицу 1.
Как следует из таблицы 1, в критической точке (0,0) локального экстремума нет. А вот в точках (1,1) и (-1,-1) имеют место локальные минимумы. Поскольку в рассматриваемом примере значения критериальной функции в точках (1,1) и (-1,-1) равны между собой, в качестве оптимального решения можно выбрать любое из двух предложенных.
Таблица 1. Расчеты критических точек
Критическая точка  | 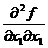 |  |  | 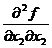 |  |  |  |  |
| (0,0) | -2 | -2 | -2 | -2 | -1 -1 | -1 -1 | -8 | |
| (1,1) (-1,-1) | -2 | -2 | -1 -1 | -1 -1 | -2 |
 2017-11-30
2017-11-30 1604
1604