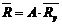Математическое ожидание несущей способности

.

Стандарт прочности материала

s(R)=s(R_y)×A.

Определим характеристику безопасности (4.9)

.

По (4.13) P =0.5+ Ф (2.64)=0.9959. Вероятность неразрушения выше, чем в первом случае, так как для разрушения и нагрузка и предел текучести одновременно должны достичь неблагоприятных значений, что менее вероятно ().

Коэффициент запаса

Иногда вместо резерва прочности вводят случайный коэффициент запаса

K=R/F, (4.15)

здесь K, R, F – случайные величины.

Тогда вероятность разрушения:

, (4.16)

где P_k(1) – функция распределения коэффициента запаса при аргументе K =1.

Вероятность неразрушения:

P=P(K>1). (4.17)

М.о. коэффициента запаса (коэффициент детерминированный)

. (4.18)

Разделим числитель и знаменатель правой части (4.9) на и используя (4.18) получим характеристику безопасности:

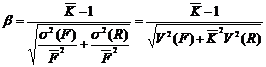, (4.19)

где 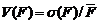, – коэффициенты вариации усилия и несущей способности.

Введение в (4.9) значений V(F) и V(R) имеет то преимущество, что они могут быть сравнительно легко оценены с достаточной точностью даже при отсутствии полных статистических данных относительно с.в. R и F. Кроме того, при изменении значения нагрузки (например, в результате увеличения площади, с которой она собирается), равно как при изменении прочности несущих элементов (например, вслед-ствие увеличения размеров поперечных сечений), коэффициенты вариации V(F) и V(R) остаются постоянными.

Из (4.19) при делении на числителя и знаменателя видно, что при , при . Можно доказать, что при увеличении от 1 до ¥ b монотонно изменяется от 0 до .