Локальная формула Лапласа

– вероятность появления события ровно раз при независимых испытаниях, 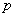– вероятность появления события при одном испытании, .

Интегральная формула Лапласа

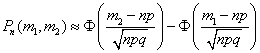– вероятность появления события не менее m₁ и не более m₂ раз при независимых испытаниях, 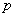–вероятность появления события при одном испытании, .

11. Оценка отклонения относительной частоты от постоянной вероятности :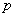

.

II. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ОСНОВНЫЕ ФОРМУЛЫ

Ряд распределения дискретной случайной величины

 

			…….
			…….

Сумма вероятностей всегда равна 1. _.

13. Функция распределения (интегральная функция распределения)

Функция распределения случайной величины определяется по формуле 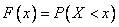. Это неубывающая функция, принимающая значения от 0 до 1. Если задана плотность распределения , то функция распределения выражается как .

Плотность распределения (дифференциальная функция распределения)

Плотность распределения случайной величины определяется по формуле . Существует только для непрерывной случайной величины. Для нее выполняется условие нормировки: (площадь под кривой равна 1).

 

Вероятность попадания случайной величины в заданный интервал

Может быть вычислена двумя способами:

1) через функцию распределения ^;

2) через плотность распределения _.