2017-12-14
331
1. Для дискретной случайной величины 
, заданной рядом распределения:
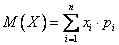
2. Для непрерывной случайной величины , заданной плотностью распределения:
Дисперсия случайной величины
По определению дисперсия – это второй центральный момент:
.
1. Для дискретной случайной величины , заданной рядом распределения:
2. Для непрерывной случайной величины , заданной плотностью распределения:
Среднее квадратическое отклонение случайной величины
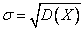
Начальный момент r-го порядка случайной величины
.
В частности, первый начальный момент – это математическое ожидание: 
Центральный момент r – го порядка случайной величины
В частности, второй центральный момент – это дисперсия: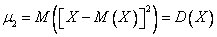 
.
Асимметрия
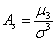
Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого (правая часть кривой более пологая), и отрицателен в противном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.
|
|
|
Эксцесс
Коэффициент эксцесса нормального распределения равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик гладкий.
III. РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН. ОСНОВНЫЕ ФОРМУЛЫ ОНЛАЙН
