 – количество «успехов» в последовательности из
– количество «успехов» в последовательности из  независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна
независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна 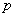 .
.  .
.
Закон распределения  имеет вид:
имеет вид:

| ….. | k | ….. | 
| ||

| 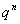
| 
| 
| 
|
Здесь вероятности находятся по формуле Бернулли:
 .
.
Характеристики:  ,
,  ,
,  .
.
Примеры многоугольников распределения для 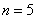 и различных вероятностей.
и различных вероятностей.

Пуассоновское распределение (дискретное)
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
При условии  закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность
закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность 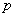 события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Ряд распределения:

| ….. | k | ….. | ||

| 
| 
| ….. | 
| ….. |
Вероятности вычисляются по формуле Пуассона:  .
.
Числовые характеристики:  ,
, 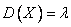 ,
,  .
.
Разные многоугольники распределения при 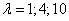 .
.

 2017-12-14
2017-12-14 346
346








