Напомним, что все члены уравнения Бернулли, выраженные в единицах длины, отнесены к единице веса движущейся жидкости.
Использовав метод размерностей, легко установить, что все эти члены могут быть выражены в единицах работы или энергии, отнесенных к единице веса жидкости.
Так
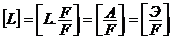 ,
,
где: L - символ длины;
F - символ силы (веса);
A - символ работы;
Э - символ энергии.
Энергия, отнесенная к единице веса, как известно, называется удельной энергией.
Таким образом, каждый из членов уравнения Бернулли представляет собой определенный вид удельной энергии движущейся жидкости. Для выявления энергетического смысла уравнения Бернулли рассмотрим вначале некоторую часть элементарной струйки массой m и объемом W, обладающей скоростью u и испытывающей гидродинамическое давление p (рис. 2 – 2).
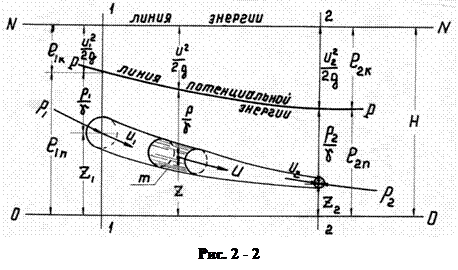
Если эта масса находится на высоте z от плоскости сравнения О - О, то потенциальная энергия массы струйки m, зависящая от положения, будет равна ее весу, умноженному на высоту поднятия, т.е. m.g.z, отсюда удельная потенциальная энергия положения будет равна:
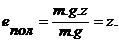
Таким образом, первый член уравнения Бернулли – z с энергетической точки зрения представляет собой удельную энергию положения движущейся жидкости.
Так как масса струйки занимает объем W и испытывает давление p, то потенциальная энергия давления будет p.W. Поскольку вес жидкости в объеме W можно выразить, как g.W, то удельная потенциальная энергия давления определится соотношением:
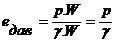 .
.
Oтсюда видно, что в энергетическом смысле член  в уравнении Бернулли представляет собой вид удельной потенциальной энергии, обусловленной гидродинамическим давлением и называемой удельной энергией давления движущейся жидкости.
в уравнении Бернулли представляет собой вид удельной потенциальной энергии, обусловленной гидродинамическим давлением и называемой удельной энергией давления движущейся жидкости.
Сумма удельных энергий положения и давления называется удельной потенциальной энергией движущейся жидкости - eп .
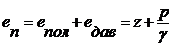 .
.
Третий член уравнения Бернулли 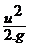 выражает собой величину удельной кинетической энергии eк движущейся жидкости.
выражает собой величину удельной кинетической энергии eк движущейся жидкости.
Действительно, кинетическая энергия, которой обладает масса m движущаяся со скоростью u будет 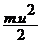 . Если же эту энергию отнести к единице веса (т.е. разделить на m.g), то легко получить, что
. Если же эту энергию отнести к единице веса (т.е. разделить на m.g), то легко получить, что
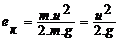 .
.
Отсюда видно, что сумма трех членов уравнения Бернулли представляет собой полную удельную энергию движущейся жидкости e, которая слагается из удельной энергии потенциальной энергии eп (равной сумме удельной энергии положения и давления) и удельной кинетической энергии eк, т.е.
 .
.
Переписав это уравнение для двух частиц (1 и 2), находящихся в одной элементарной струйке, или для двух положений одной и той же частицы движущейся жидкости, мы заметим, что
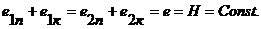 (1 – 9)
(1 – 9)
Т.е. сумма удельной потенциальной и кинетической энергии по длине элементарной струйки остается постоянной.
Уравнение Бернулли в форме (1 – 8) или (1 – 9) позволят четко определить взаимосвязь между удельной потенциальной и кинетической энергией и преобразованием одного вида энергии в другой (например части потенциальной энергии в кинетическую или наоборот). Поэтому уравнение Бернулли представляет собой частное выражение общего закона сохранения энергии.
Резюмируя сказанное выше, энергетический смысл уравнения Бернулли можно кратко сформулировать следующим образом: при установившемся движении идеальной жидкости удельная энергия не изменяется по длине элементарной струйки.
Уравнение Бернулли для элементарной струйки реальной жидкости
При движении реальной жидкости следует учитывать ее вязкость, вследствие которой возникает сопротивление движению частиц (т.е. силы трения). На преодоление сил трения затрачивается часть энергии жидкости.
Поэтому удельная энергия жидкости в сечении элементарной струйки 2-2 (рис. 2-3) (e2 или H2 будет меньше удельной энергии жидкости в сечении 1-1 (e1 или H1)на некоторую величину h¢, равную
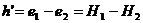 . (1 – 10)
. (1 – 10)
Отсюда, с учетом выражения (1 – 9), получим уравнение Бернулли для элементарной струйки реальной жидкости в следующем виде:
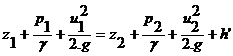 , (1 – 11)
, (1 – 11)
где h’ - удельная энергия жидкости (или напор), затрачиваемая на преодоление гидравлических сопротивлений в пути между 1-ым и 2-ым сечением элементарной струйки. Как и все члены уравнения, член h’ имеет размерность длины.
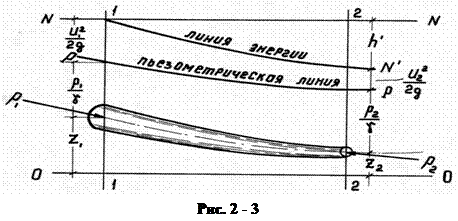
Графическое изображение уравнения Бернулли для рассматриваемого случая представлено на рис. 2 - 1.
Для струйки реальной жидкости сумма высот геометрической, пьезометрической и скоростной уже не остается постоянной, а убывает по длине струйки, что выражается отклонением напорной линии N – N’ от горизонтальной линии N - N. Величина отклонения представляет собой потерю напора или удельной энергии на соответствующем участке элементарной струйки. Линия N – N’, характеризующая величику.удельной энергии жидкости в любой точке элементарной струйки, называется линией энергии. Линия p – p называется пьезометрической линией.
 2017-12-14
2017-12-14 3992
3992
