Понятие первообразной, неопределенного интеграла

Определение. Функция F (х)называется первообразной функцией для функции f (х) на промежутке X, если в каждой точке х этого промежутка .

Например, –является первообразной для функции , так как .

Рисунок 13 – График кривой у = F (х)

По геометрическому смыслу производной 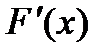есть угловой коэффициент касательной к кривой у = F (х) в точке с абсциссой х. Геометрически найти первообразную для f (х) – значит найти такую кривую у = F (х), что угловой коэффициент касательной к ней в произвольной точке х равен значению f (х) заданной функции в этой точке (см. рис. 13).

Следует отметить, что для заданной функции f (x)ее первообразная определена неоднозначно. Дифференцируя, нетрудноубедиться, что функции и вообще где C – некоторое число, являются первообразными для функции . Аналогично в общем случае, если F (x)– некоторая первообразная для f (х), то, поскольку , функции вида F (х) + С, где С – произвольное число, также являются первообразными для f (х).

Геометрически это означает, что если найдена одна кривая у = F (х), удовлетворяющая условию , то, сдвигая ее вдоль оси ординат, мы вновь получаем кривые, удовлетворяющие указанному условию (поскольку такой сдвиг не меняет углового коэффициента касательной в точке с абсциссой х) (см. рис. 13).

Теорема. Если F ₁(х) и F ₂(х) –первообразные для функции f (x)на некотором промежутке X, то найдется такое число С, что будет справедливо равенство F ₂(х) = F ₁(х) + С.

Из данной теоремы следует, что, если F (х) — первообразная для функции f (x), то выражение вида F (х) + С,где С – произвольное число, задает все возможные первообразные для f (х).

Определение. Совокупность всех первообразных для функции f (х)на промежутке X называется неопределенным интегралом отфункции f (х) и обозначается , где – знак интеграла, f (х) – подынтегральная функция,f (х) dx–подынтегральное выражение. Таким образом,