Одноразмерные матрицы можно складывать.
Алгебраической суммой двух матриц Am´n=(aij) и Bm´n=(bij) называется матрица Cm´n=(cij)такая, что cij= aij+ bij (i=1,2..m, j=1,2…n)
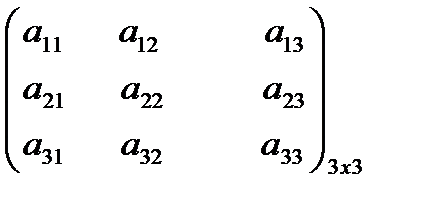
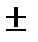
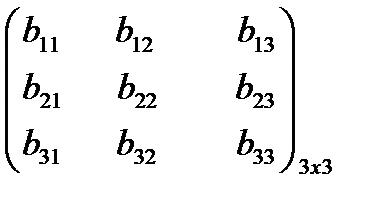 =
=
= 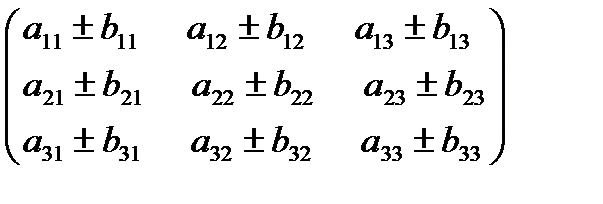
Пример:
А= 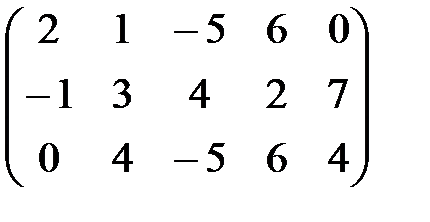 В=
В= 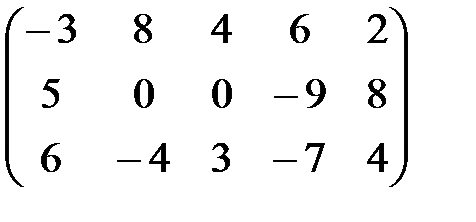
С=А+В= 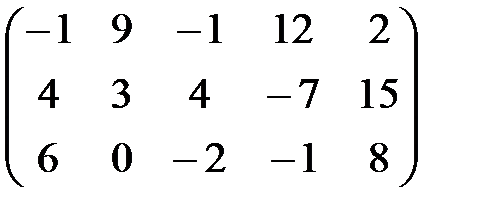
Операция сложения одноразмерных матриц обладает следующими свойствами:
-коммутативность (переместительный закон) А+В=В+А
-ассоциативность (сочетательный закон)
(А+В)+С=А+(В+С)=А+В+С
- А+ 0 =А
Произведением матрицы Am´n=(aij) на число k называется матрица
Bm´n=(bij) такая, что bij= kaij(i=1,2..m, j=1,2…n). Т.е. Произведением числа k на матрицу А называется матрица, определяемая равенством:
k 
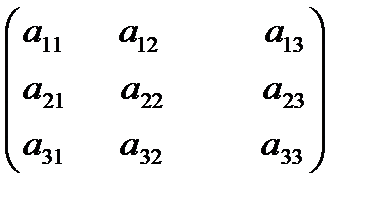 =
= 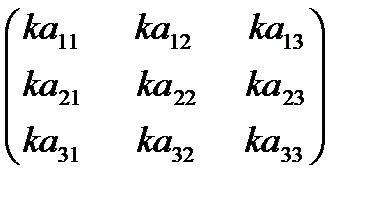
Пример:
А= 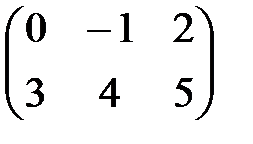 , число k=2, 2А=
, число k=2, 2А= 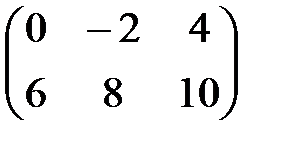
Матрица (–А), все элементы которой получены путем умножения соответствующих элементов матрицы А на (-1) называется матрицей противоположной А.
Умножение матрицы на число обладает следующими свойствами:
- 1×А=А
- k×(А+В)=k×А+k×В
-(a+b)×А=a×А+b×А
-(ab)×А=a×(bА)
- А+(- А)= 0
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы Am´n=(aij) на матрицу Вn´p=(bjk) называется матрица Сm´p=(cik) такая, что cik=ai1×b1k+ai2×b2k+…+ain×bnk, где i=1,2..m, k=1,2,..
…p, т.е. элемент i-й строки и k-ого столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-ого столбца матрицы В.
Иными словами: Произведение двух матриц А и В обозначается символом АВ и определяется равенством:
AB = 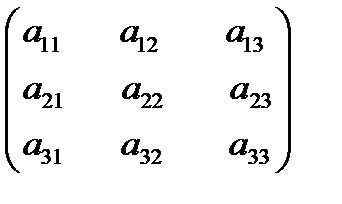

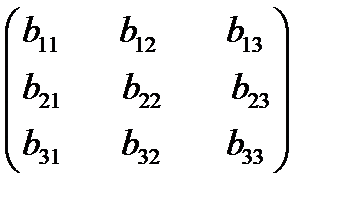 =
=
= 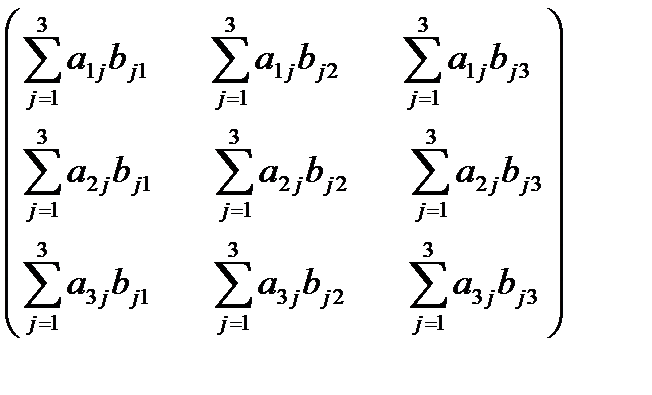
Пример: А= 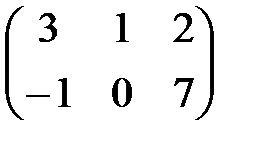 В=
В= 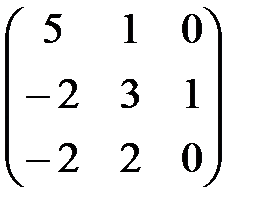 С=А×В=
С=А×В= 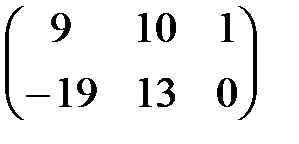
с11=3×5+1×(-2)+2×(-2)=9
с12=3×1+1×3+2×2=10
с13=3×0+1×1+2×0=1
с21=-1×5+0×(-2)+7×(-2)=-19
с22=-1×1+0×3+7×2=13
с23=-1×0+0×1+7×0=0
Если матрицы А и В - квадратные одного размера, то произведения АВ и ВА всегда существуют.
Умножение матриц обладает следующими свойствами:
- АВ¹ВА, если данное равенство выполняется, то матрицы А и В называют перестановочными (обладают свойством коммутации);
- А×(В×С)= (А×В)×С (ассоциативность);
- А×(В+С)=АВ+АС (дистрибутивность умножения относительно сложения);
- А×Е=А
- a×(АВ)= (a×А)В.
Матрица, полученная из данной заменой каждой ее строк столбцами с с сохранением нумерации, называется матрицей транспонированной к данной. Обозначается АТ (А¢).
Пусть дана матрица Аn´m= 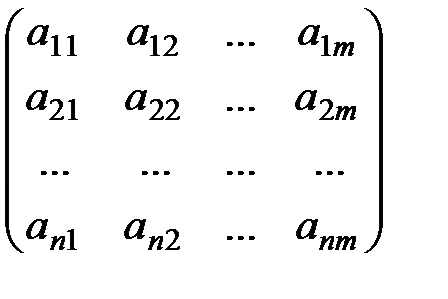 , тогда
, тогда
AТm´n= 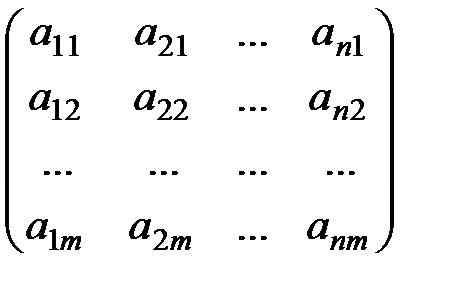
Пример: Вычислить матрицу: D=A×BT – 2E + C2,
если 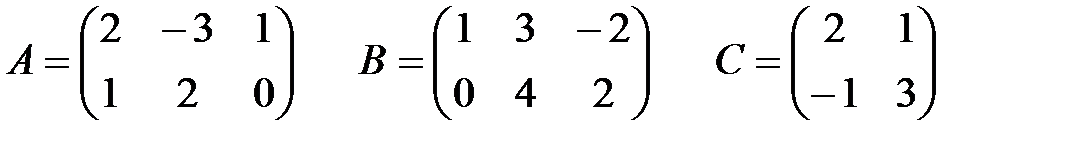
Решение:
1. Составим матрицу ВТ, поменяв строки и столбцы матрицы В местами с сохранением нумерации ВТ= 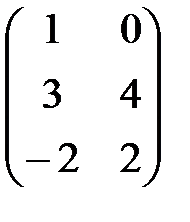
2. Найдем произведение матриц A×BT
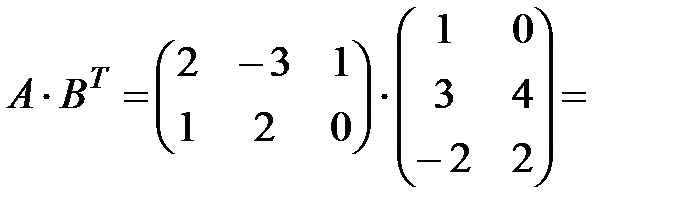
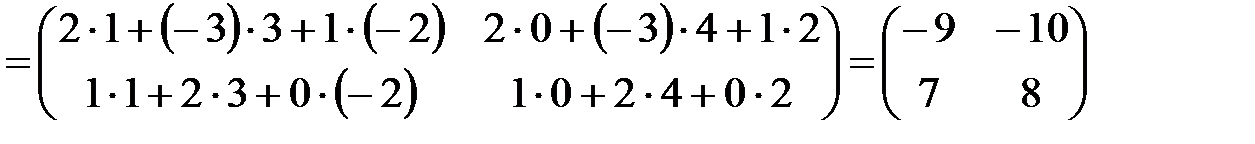
3. Найдем произведение 2×Е= 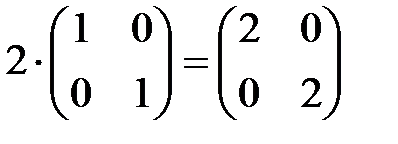
4. Найдем матрицу С2= С×С
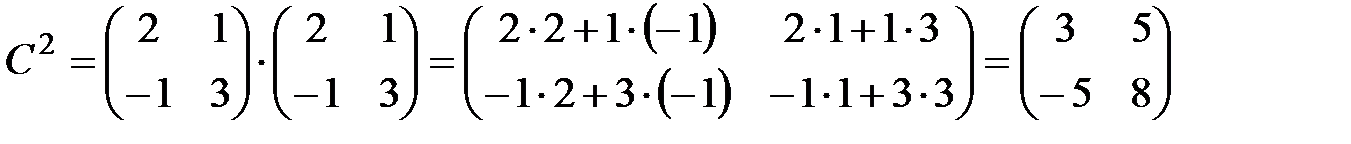
5. Найдем матрицу D=A×BT – 2E + C2, подставив найденные матрицы
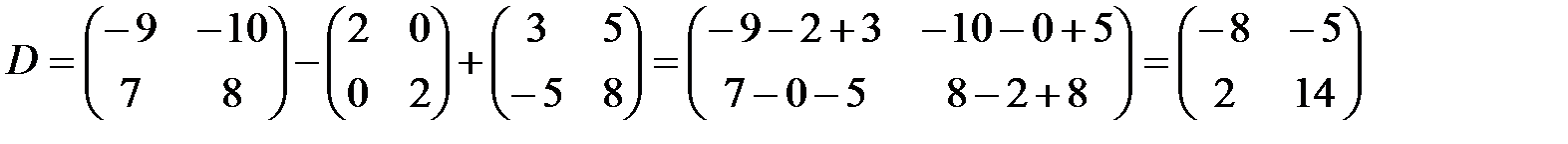
Ответ: 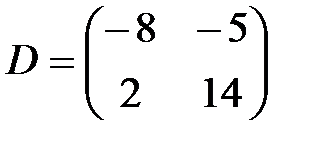
Пример: А= 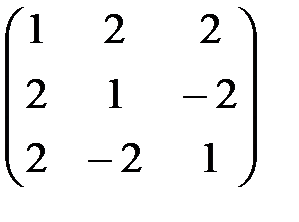 . Найдём обратную матрицу для А с помощью элементарных преобразований.
. Найдём обратную матрицу для А с помощью элементарных преобразований.
Для этого припишем к матрице А единичную матрицу и будем применять элементарные преобразования к обеим матрицам А и Е так, чтобы на месте матрицы А получить единичную матрицу. Тогда на месте единичной матрицы получится обратная матрица А-1.
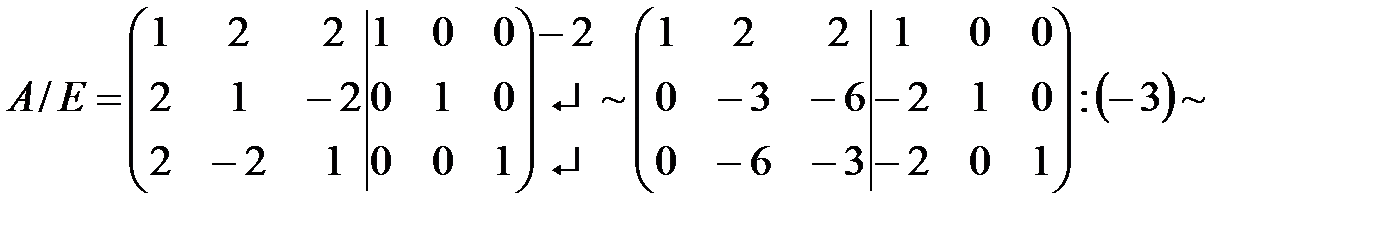
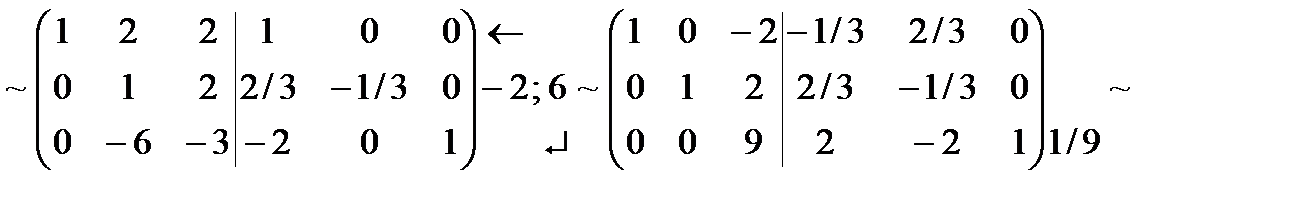
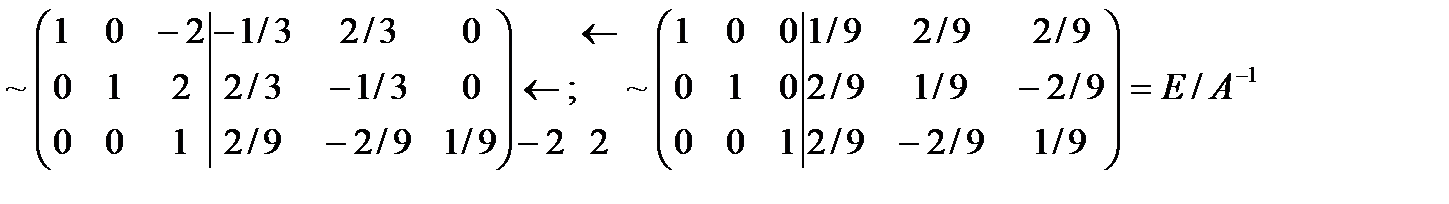
Итак, нашли 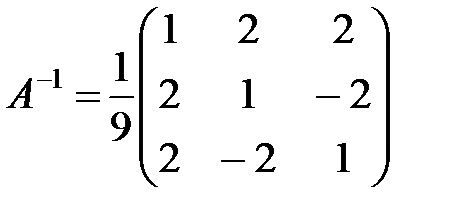 .
.
 2017-12-14
2017-12-14 1311
1311
