1. Определитель не изменяется, если его строки поменять местами с соответствующими столбцами,
2. При перестановки двух строк (или столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину.
3. Определитель с двумя одинаковыми сроками (столбцами) равен нулю.
4. Общий множитель всех элементов строки или столбца можно вынести за знак определителя;
5. Если все элементы какой-то строки или столбца равны 0, то и определитель равен 0.
6. Если все элементы какой-то строки (столбца) пропорциональны элементам другой строки (столбца), то определитель равен 0.
Теорема о существовании обратной матрицы: Квадратная матрица имеет обратную тогда и только тогда, кода ее определитель отличен от нуля.
Матрица, у которой определитель отличен от нуля, называется невырожденной, в противном случае она вырождена.
3. Системы линейных уравнений, методы решения.
Структура вида
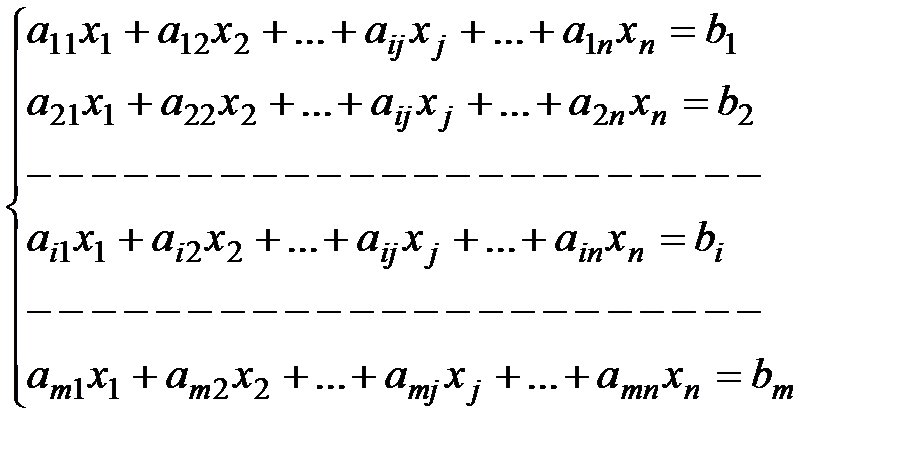 ,
,
где аij, bi (i=1,2,…m) (j=1,2,…n) – произвольные числа:
аij – коэффициенты при переменных хj;
bi – свободные члены,
называется системой m линейных уравнений относительно n неизвестных.
Решением системы m линейных уравнений относительно n неизвестных называется упорядоченный набор чисел (кортеж) (x1,x2,…xn) при подстановке которых каждое уравнение системы обращается в истинное числовое равенство.
Решить систему - значит, найти множество всех ее решений.
Система может иметь а) единственное решение; б) бесконечное множество решений; в) пустое множество решений.
Система, имеющая хотя бы одно решение, называется совместной.
Система, имеющая пустое множество решений, называется несовместной.
Совместная система, имеющая единственное решение, называется определенной.
Совместная система, имеющая бесконечное множество решений, называется неопределенной.
Две системы называются равносильными, если они имеют одно и то же множество решений.
Рассмотрим элементарные преобразования, позволяющие получить систему, равносильную данной:
а) перестановка уравнений;
б) вычеркивание из системы уравнения вида 0х1+0х2+…+0хn=0;
в) умножение обеих частей, какого то уравнения на одно и то же число, отличное от нуля;
г) прибавление к обеим частям одного из уравнений соответствующих частей другого уравнения, умноженных на одно и тоже число.
Метод Гаусса
Рассмотрим решение системы методом Гаусса на конкретном примере:
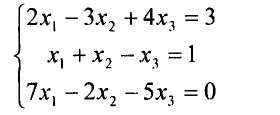
Метод Гаусса заключается в том, что с помощью элементарных преобразований система приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последнего, находятся значения переменных.
Составим расширенную матрицу из коэффициентов при переменных и свободных членов, поменяв первую и вторую строку, чтобы а11=1
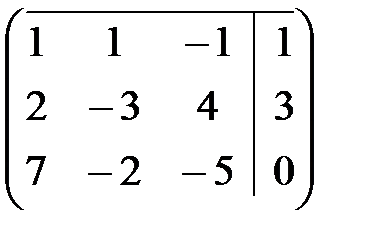
Умножим элементы первой строки на -2 и прибавим к соответствующим элементам второй строки, умножим элементы первой строки на -7 и прибавим к соответствующим элементам третьей строки. В результате получим в первом столбце, во второй и третьей строке 0
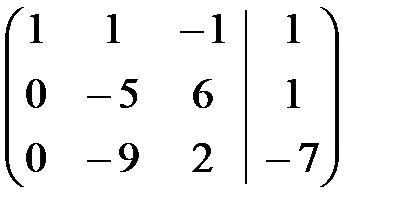
Умножим элементы второй строки на -9 а элементы третьей на 5 и полученные элементы второй строки прибавим к соответствующим элементам третьей строки, тогда получим:

Запишем преобразованные уравнения:

Теперь можно найти значения переменных, подставляя последовательно значение х3 во второе уравнение, найдем х2, подставим значения х2 и х3 в первое уравнение найдем х1

Ответ: {(1;1;1)}
Пример:
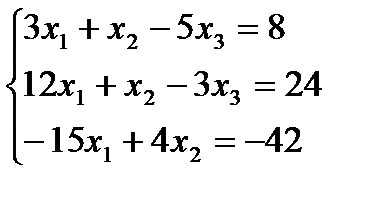
Исключим x1 из всех уравнений, кроме первого. Для этого мы должны прибавить ко второму уравнению первое, умноженное на (- 4), а к третьему прибавить первое, умноженное на 5.

Получим систему равносильную исходной.
На втором шаге исключения мы не трогаем первое уравнение. Другие два уравнения содержат два неизвестных х2 и х3 и к ним можно применить ту же процедуру исключения. Для этого к третьему уравнению прибавляем первое, умноженное на 3.

Вновь получим систему равносильную исходной.
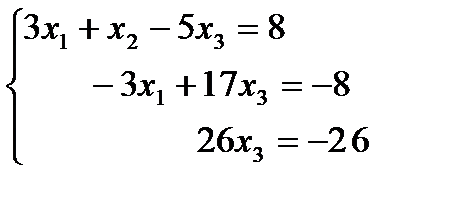
Далее наши действия очевидны. Из третьего уравнения х3 = -1, подставляя значения х3 во второе уравнение, получаем х2 = -3 и, наконец, из первого уравнения получаем х1= 2.
Если в результате преобразований получим уравнение, в котором все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля, то полученное уравнение, а следовательно, и вся система несовместны, если же свободный член равен нулю, то система является неопределенной.
Решите предложенные системы методами Крамера и Гаусса.

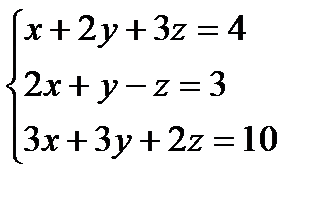
Ответ: (2;-1;-3)Ответ: система несовместна.
 2017-12-14
2017-12-14 1231
1231
