Каждой квадратной матрице А соответствует число - определитель данной матрицы  (det А).
(det А).
A= 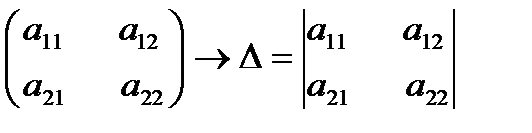 - определитель второго порядка.
- определитель второго порядка.
B= 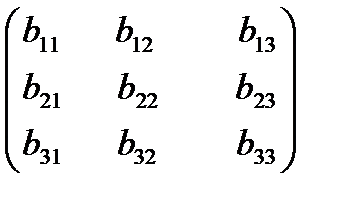
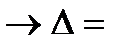
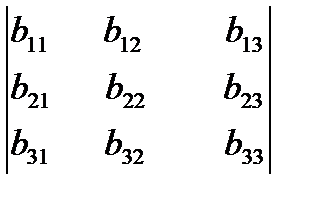 - определитель третьего порядка
- определитель третьего порядка
Для вычисления определителя второго порядка используют формулу:
A= 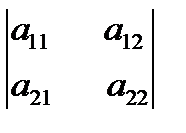 =
= 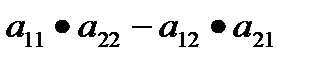
Пример:
1) А=(а11) матрица 1-ого порядка
D1=| а11|= а11 | 7|=7 | -3|=-3
2) А= 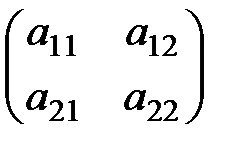 матрица 2-ого порядка
матрица 2-ого порядка
D2= 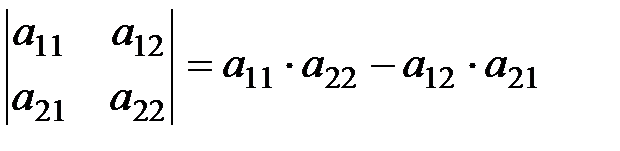
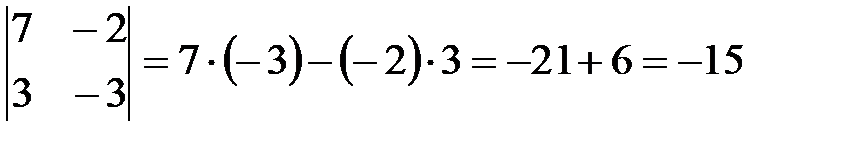
Определителем третьего порядка называют число, обозначаемое символом
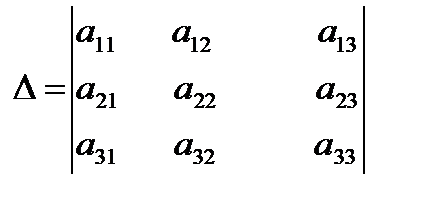
и определяемое равенством
 =
= 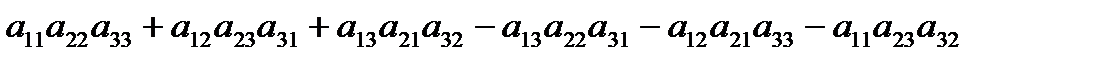 (2)
(2)
Определитель 3-его порядка можно вычислить по правилу треугольника, схеме Саррюса.
Чтобы запомнить, какие произведения в правой части равенства (2) берутся со знаком «+», а какие со знаком«—», полезно использован следующее правило треугольников:
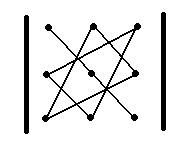
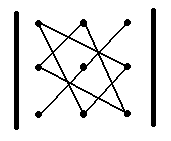
«+» «-»
Это правило позволяет легко записать формулу (2) и вычислить данный определитель.
А= 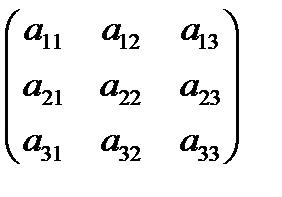 матрица 3-его порядка
матрица 3-его порядка
Правило треугольника:
D3= 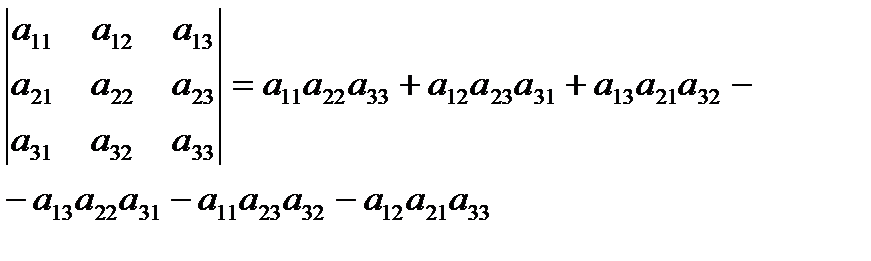
Пример:
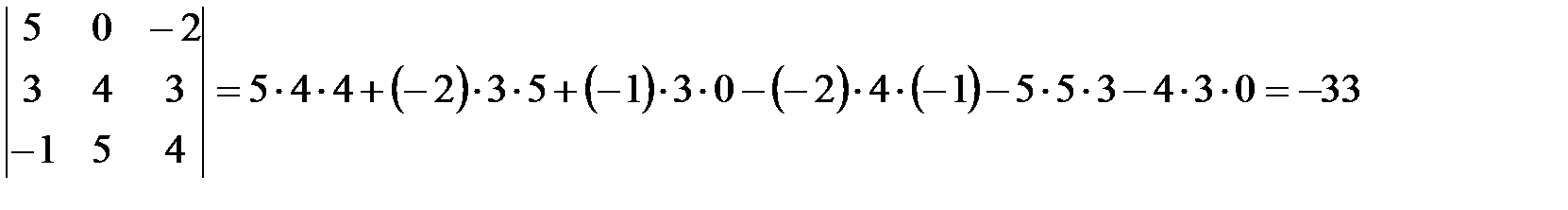
 2017-12-14
2017-12-14 1881
1881
