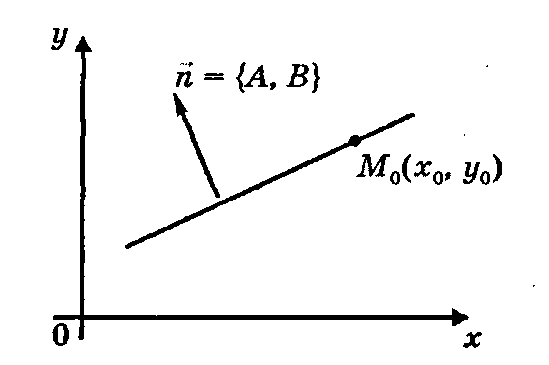Уравнение прямой на плоскости, способы задания прямой на плоскости

Если на плоскости произвольно введена декартова система координат, то всякое уравнение первой степени относительно текущих координат х и у

А х + В у + С =0,

где А и В одновременно не равны нулю, определяют прямую в этой системе координат.

1) 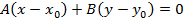- уравнение прямой, проходящей через точку 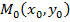перпендикулярно нормальному вектору ;

2) Ax+By+C=0 – общее уравнение прямой;

3) 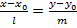– уравнение прямой, проходящей через точку 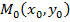параллельно направляющему вектору {каноническое уравнение прямой);

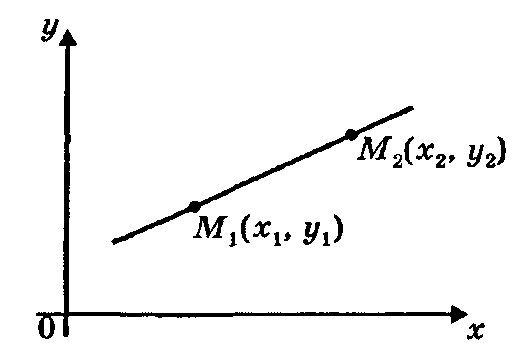4) 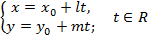– параметрические уравнения прямой;

5) 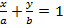– уравнение прямой в отрезках, где a и b – величины направленных отрезков, отсекаемых на координатных осях Ох и Оу соответственно;

6) – уравнение прямой, проходящей через две данные точк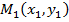и и ;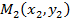

7) 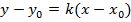– уравнение прямой, проходящей через точку 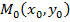, k - угловой коэффициент прямой, равный тангенсу угла наклона прямой к положительному направлению оси Ох;