2017-12-14
735
Распространенным методом минимизации функций большого числа переменных является метод градиентного спуска. Последующее приближение получается из предыдущего смещением в направлении, противоположном градиенту функции F(x). Каждое следующее приближение ищется в виде
.
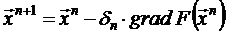Приведенное описание не определяет алгоритм однозначно, т.к. ничего не сказано о выборе параметра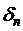 
. Его можно определять из условия минимума величины 
.
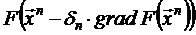В этом случае рассматриваемый метод называют методом наискорейшего градиентного спуска.
Для функции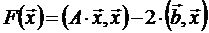 
, соответствующей системе линейных уравнений с матрицей 
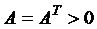, задача нахождения минимума решается в явном виде
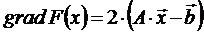
так как
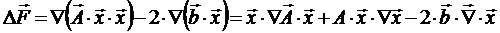
и
.
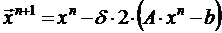Обозначим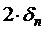 
через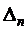 
, т.е.
.
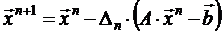Предположим, что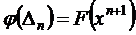 
. Учитывая, что 
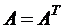, вычислим 
:
,
.
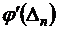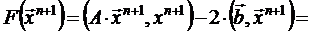
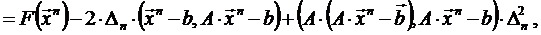
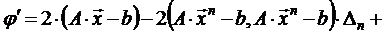
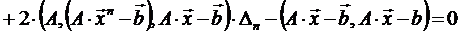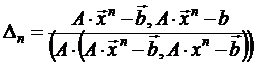ЛЕКЦИЯ 6. ИНТЕРПОЛИРОВАНИЕ И ЭКСТРАПОЛИРОВАНИЕ
1. Математическая постановка задачи интерполирования.
В экономике и технике, часто приходится сталкиватьcя с необходимостью вычисления значений функции у = f(х) в точках, отличных от значения аргумента, фиксированных в таблице.
Подобные задачи практики формализуются как математические задачи интерполирования.
Пусть на отрезке [a, b] задана функция у = f(х) своими n + 1 значениями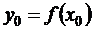 
; 
; …; 
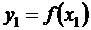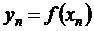в точках x 0, x 1, …, xn , которые назовем узлами интерполяции.
Требуется найти аналитическое выражение табулированной функции F(х), совпадающее в узлах интерполяции со значениями заданной функции,
| y 0 | y 1 | … | yn- 1 | yn |
| x 0 | x 1 | … | xn- 1 | xn |
т.е.
; 
; …; 
.
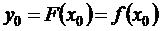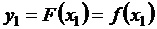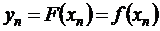Процесс вычисления значений функций в точках х, отличных от узлов интерполяции, называется интерполированием функции f(х).
Если аргумент х находится за пределами отрезка интерполирования [x 0, xn], то задача определения значения функции в точке х называется экстраполированием.
Задача становится однозначной, если в качестве интерполирующей функции f(х) для функции у = f(х), заданной своими n+ 1 значениями, выбрать многочлен Fn (x) степени не выше n, такой, что
; 
; …; 
.
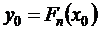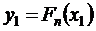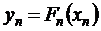Многочлен Fn(x) удовлетворяющий этим условиям, называют интерполяционным многочленом, а соответствующие формулы – интерполяционными.
В случае, когда F(x) выбирается в классе степенных функций, интерполяция называется параболической.
При интерполировании возникает ряд задач:
1. Выбор наиболее удобного способа построения интерполяционной функции для каждого конкретного случая.
2. Оценка погрешности при замене f(x) интерполирующей функцией F(x) на отрезке [a, b].
3. Оптимальный выбор узлов интерполяции для получения минимальной погрешности.
