2017-12-14
2384
А). Метод простой итерации.
Представим уравнение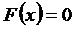 
через 
и многократным применением формулы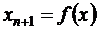 
до тех пор, пока 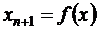не даст 
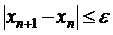, где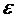 
– заданная погрешность вычисления.
б). Метод деления отрезка пополам (Дихотомии).
Для 
:
1. находим 
;
2. вычисляем 
;
3. если 
, задаем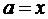 
, иначе 
.
4. Проверяем условие 
: если оно выполняется, идем к п.1., если не выполняется, заканчиваем вычисление и считаем, что 
приблизительно равен искомому решению исходного уравнения с заданной точностью .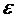
Число итераций при использовании этого метода
.
в). Метод Хорд.
Пусть имеем уравнени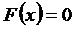е , где - непрерывная функция на 
, имеющая непрерывные 
и 
.
Корень считается отделенным и находится на отрезке 
, т.е.
Уравнение хорды проходящей через точку А 0 и В (см. рис.5.1, рис.5.2)
 |
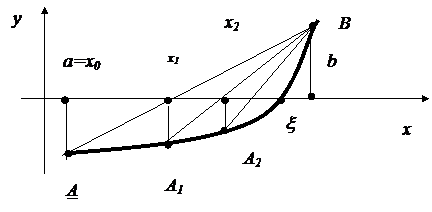Рис. 5.1
 |
Рис. 5.2
имеет вид
.
Найдем х = х 1, для которого y = 0
.
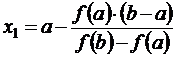Если корень нас не устраивает, то мы находим
;
;
...
.
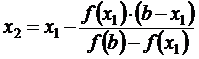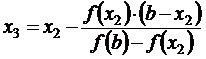Рассмотрим случай, когда первая и вторая производные имеют разные знаки. (рис.5.3):
, 
.
 |
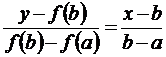Рис. 5.3
,
,
...
.
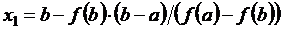Неподвижными концами отрезка является тот, для которого знак функции совпадает со знаком второй производной 
.
Г). Метод Ньютона.
Пусть корень уравнения f(x) = 0 отделен на отрезке [a, b], причем и непрерывны и сохраняют постоянные значения на всем отрезке [a, b].
Геометрический смысл метода Ньютона в том, что дуга кривой y = f(x) заменяется касательной к этой кривой.
Первый случай (рис.5.4):
f(a) < 0, f(b) > 0, > 0, > 0(основная линия)
или
f(a) > 0, f(b) < 0, < 0, < 0(пунктирная линия).
 |
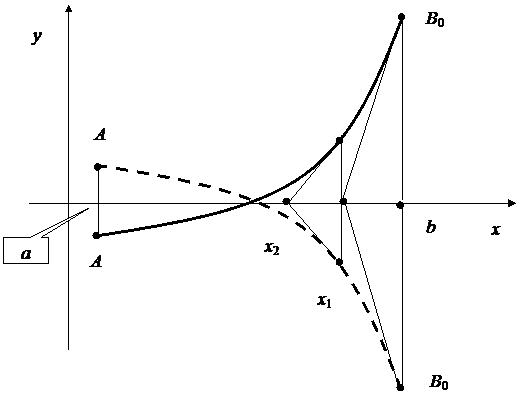Рис. 5.4
Проведем касательную к кривой y = f(x) в точке B 0
.
Полагая y = 0, x = x 1 , получим
,
,
...
.
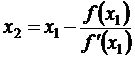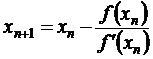Второй случай (рис. 5.5):
f(a) < 0, f(b) > 0, > 0, < 0(основная линия)
или
f(a) > 0, f(b) < 0, < 0, > 0(пунктирная линия),
.
 |
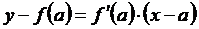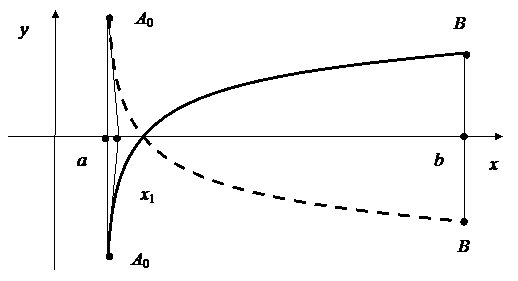Рис. 5.5
Полагая y = 0, х = х 1, получим
, ,..., .
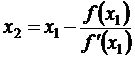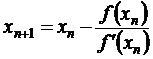При выборе начального приближения корня необходимо руководствоваться правилом: за исходную точку следует выбирать тот конец [a, b], в котором знак функции совпадает со знаком 
, т.е.
, a = x 0 .
д). Модифицированный метод Ньютона.
Заключается в том, что вместо вычисления производной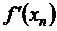 
на каждом шаге итераций находится ее приближенное значение
, 
.
Следовательно, итерационная формула имеет вид
.
Значение 
не обязательно должно быть постоянно. Равенство 
позволяет уменьшить число исходных данных при вводе.
Метод Рыбакова
Можно рассматривать этот метод как модификацию метода Ньютона. При замене 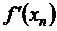некоторым числом 
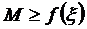, где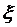 
– значение х на [a, b], при котором производная максимальна.
При 
сходимость не нарушается, но замедляется.
Метод Рыбакова удобен для поиска всех корней уравнения f(x) = 0 на [a,b].
1. Задаем начальные значения х = х 0 = а.
2. Для каждой последовательной итерации (n = 0, 1, 2, …) вычисляем
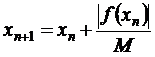
и проверяем условие xn < b, если оно выполняется, то, значит, найдены все корни, в противном случае проверяем выполнение условия 
. Если оно не выполняется, то повторяем цикл с пункта 2 и переходим к пункту 3.
3. Задаем начальное приближение 
и снова идем на пункт 2.
