Шар в равномерном поле

Если в равномерное поле, напряженность которого равна Е₀ (рис. 11.19), внести металлический или диэлектрический шар (e шара отлично от e окружающей среды), то электрическое поле, в особенности вблизи от шара, исказится, перестанет быть равномерным. Характер искажения поля зависит от размеров шара, от его e и от величины заряда на шаре.

Если шар металлический, то силовые линии должны подходить к его поверхности под прямым углом. Если металлический шар не заряжен, то на нем вследствие явления электростатической индукции произойдет разделение зарядов. Силовые линии будут заканчиваться или начинаться на них. Металлический шар может быть и заряжен, т. е. нести на себе избыточный заряд, который также расположится на поверхности. Если шар из диэлектрика, то под влиянием внешнего по отношению к нему поля шар поляризуется. Заряды, выявившиеся на шаре вследствие поляризации, исказят прежде (до внесения шара) равномерное поле. Силовые линии будут подходить к поверхности шара так, что будут выполняться два граничных условия. Эта задача является одной из наиболее типичных «классических» задач. Если шар металлический, то внутри шара Е = 0 и j = const. Вне зависимости от того, металлический шар или диэлектрический во внешней по отношению к шару области нет свободных зарядов, и потому поле в наружной по отношению к шару области описывается уравнением Лапласа. Если шар из диэлектрика и свободный заряд на нем равен нулю, то поле внутри шара описывается также уравнением Лапласа. Таким образом, для решения той и другой задачи необходимо проинтегрировать уравнение Лапласа Ѳj=0. Любая конкретная задача на интегрирование уравнения Лапласа в качестве первого этапа предполагает правильный выбор системы координат. Система координат должна быть выбрана таким образом, чтобы граничные поверхности в поле описывались наиболее удобным образом.

 

Рис. 11.19. Шар в равномерном электрическом поле.

 

В нашей задаче граничная поверхность — сфера. Сфера наиболее удобно описывается в сферической системе координат. Поэтому будем пользоваться сферической системой координат.

Вторым этапом решения является выяснение вопроса о том, не обладает ли изучаемое поле тем или иным видом симметрии. Условия симметрии поля часто в значительной мере облегчают решение задачи. В рассматриваемой задаче поле не зависит от координаты a. Чтобы убедиться в этом, поступим следующим образом. Мысленно рассечем поле плоскостью, перпендикулярной оси Z декартовой системы, и проведем в этой плоскости окружность так, чтобы центр ее лежал на оси Z. Все точки этой окружности имеют одно и то же значение радиуса R, соединяющего точку на этой окружности с началом координат, и, кроме того, угол q в меридианной плоскости между радиусом R и осью Z один и тот же.

Все точки окружности находятся в поле в одинаковых условиях. Поэтому потенциал их один и тот же. Но значение угла a, характеризующего положение точек этой окружности, различно. Если для совокупности точек, обладающих R=const и q=const и различными значениями угла a, j одно и то же, то это означает, что в данном поле j не зависит от угла a. Поэтому поле будет описываться уравнением (см. уравнение 11.32):

(11.49)

(составляющая выпала, так как j не зависит от a). Уравнение (11.49) представляет собой уравнение в частных производных. Для интегрирования уравнений в частных производных применяется метод Фурье — Бернулли. Согласно методу Фурье — Бернулли решение для искомой функции (в нашем случае для j) полагается в виде произведения двух пока неизвестных функций М и N, одна из которых (М) зависит только от R, другая (N) только от q:

j=M(R)N(q)=MN. (11.50)

Вид функций М и N подлежит определению. Принятие решения в виде произведения двух функций (11.50) позволяет разбить уравнение в частных производных (11.46) на два обыкновенных дифференциальных уравнения, из которых одно составлено будет относительно M, другое- относительно N. Подставим (11.50) в (11.49)

; .

Поэтому

. (11.51)

Умножим (11.51) на

. (11.52)

Особенностью уравнения (11.52) является то, что первое слагаемое в нем представляет собой функцию только R, а второе слагаемое функцию только q. Сумма двух функций, из которых одна зависит только от R, а другая только от q, равна нулю для бесчисленного множества пар значений R и q (уравнение (11.52) годится для всех точек поля). Это может быть либо тогда, когда каждая из этих функций равна нулю

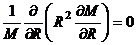и , (11.52^’ )

либо когда

(11.52^’’ )

Здесь р есть некоторое число, пока неизвестное.

Таким образом, задача свелась к интегрированию уравнений (11.52') и (11.52"). Общее решение для j будет равно согласно (11.50) произведению решений уравнений (11.52') плюс произведение решений для М и N по уравнению (11.52"). Найдем решение уравнений (11.52'). Так как в (11.52') М зависит только от R, а N только от q, то от частных производных можно перейти к простым:

Интеграл первого из них

. (11.53)

Найдем интеграл второго уравнения

;

или

N=A₃ln tg q/2 +A₄ . (11.54)

Покажем, что A₃, непременно должно равняться нулю, так как только в этом случае в решении отсутствует слагаемое

А₃ ln tg q/2.

Потенциал есть функция непрерывная и на конечном отрезке он не может измениться на бесконечно большую величину. Из физических соображений ясно, что потенциал точек оси Z вблизи шара не может быть равен бесконечности. Между тем, если бы А₃¹0, то в выражении для потенциала присутствовало бы слагаемое А₃lntgq/2, которое равно -¥ для всех точек у которых q=0 (tgq=0; lntgq= -¥).

Таким образом, частное решение для j, вытекающее из (11.52'), таково

j= C₁/R +C_2, (11.55)

 

(C₁=A₁A₄; C₂=A₂A₄).

Найдем решение уравнений (1.52")

Применим подстановку Эйлера: M=CRⁿ

; .

Подставим производные в уравнение

или

n²+ n - p=0.

Решение квадратного уравнения

. (11.56)

Значение р определим при интегрировании второго уравнения (11.52^’’ )

Решением его является выражение N = Вcosq. Убедимся в этом путем подстановки и одновременно найдем значение р;

; .

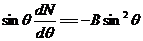Следовательно,

р = 2.

После нахождения числа р подставим его в (1.56) и найдем

n₁ = 1 и n₂= - 2.

Таким образом, совместное решение уравнений (1.52") дает следующее выражение для j:

.

Полное решение

. (11.57)

В (11.57) присутствуют четыре неизвестных постоянных С₁, C₂, С₃ и С₄. Значения постоянных зависят от того, какой шар (проводящий или диэлектрический) внесен в поле.