Уравнения Максвелла для проводящей среды. Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью g и магнитной проницаемостью mа. Обратимся к первому и второму уравнениям Максвелла, записанным в комплексной форме для синусоидально изменяющихся во времени Е и Н:

и

В проводящей среде даже при очень высоких частотах произведение weа много меньше проводимости g. Поэтому с большой степенью точности слагаемым  в первом уравнении Максвелла для проводящих сред можно пренебречь.
в первом уравнении Максвелла для проводящих сред можно пренебречь.
В настоящее время наука не располагает точными данными о числовом значении электрической проницаемости e для металлов. Имеются лишь сведения, что порядок e для металлов такой же, как и для большинства диэлектриков (т. е. от нескольких единиц до нескольких десятков). В качестве примера возьмем e для меди, равное 10, и найдем, во сколько раз ток проводимости в ней будет больше тока смещения при w = 103 и при w = 108 рад/с. При w = 103
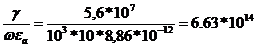 ,
,
при w = 108
 ,
,
т. е. в рассмотренном числовом примере даже при w = 103 ток проводимости больше тока смещения в 6,33·109 раз. Таким образом, первое и второе уравнения Максвелла для проводящей среды приобретают вид:
 (14.14)
(14.14)
и
 . (14.15)
. (14.15)
Эти два уравнения представляют собой уравнения с двумя неизвестными  и
и  . Решим их совместно. С этой целью возьмем ротор от уравнения (14.14):
. Решим их совместно. С этой целью возьмем ротор от уравнения (14.14):  . Учтем, что div
. Учтем, что div  = 0, и поэтому grad div
= 0, и поэтому grad div  = 0. Вместо rot
= 0. Вместо rot  подставим
подставим  . Получим
. Получим
 . (14.16)
. (14.16)
Уравнение (14.16) является дифференциальным относительно  .
.
В общем случае, когда  зависит от всех трех или даже только от двух координат, решение (14.16) довольно сложно.
зависит от всех трех или даже только от двух координат, решение (14.16) довольно сложно.
Глубина проникновения и длина волны. Под глубиной проникновения D понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором амплитуда падающей волны Е (или Н) уменьшается в е = 2,71 раз. Глубину проникновения определяют с помощью выражения: е -kD = e -1. Отсюда следует, что k D = 1 или
D =1/k. (14.17)
Глубина проникновения зависит от свойств проводящей среды (g и m) и частоты w. Так, если электромагнитная волна имеет частоту f = 5000 Гц и проникает в проводящую среду, у которой g = 107 (Ом·м)-1 и m = 103 (m не зависит от величины Н), то
 .
.
Глубина проникновения D = 1/ k» 7·10-5 м, т. е. на расстоянии в 0,007 см амплитуды Н и Е снизились в 2,71 раза.
Под длиной волны l в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором фаза колебания изменяется на 2p. Длину волны определяют из уравнения l k = 2p, отсюда:
 . (14.18)
. (14.18)
Для рассмотренного числового примера -  0,000445 м.
0,000445 м.
Иногда пользуются понятием фазовой скорости распространения электромагнитной волны в проводящей среде.
Под фазовой скоростью понимают скорость, с которой надо было бы, перемещаться вдоль оси z, чтобы колебание имело одну и ту же фазу. Фаза колебания определяется выражением w t — kz + ya.
Производная от постоянной есть нуль, поэтому  (wt — kz + ya) = 0
(wt — kz + ya) = 0
или
 ;
;  ;
;  . (14.19)
. (14.19)
Для рассмотренного числового примера uфаз =  2,25 м/с.
2,25 м/с.
Магнитный поверхностный эффект. В качестве примера распространения плоских электромагнитных волн в проводящей среде рассмотрим поле в стальном листе при прохождении вдоль листа переменного магнитного потока  . Лист (рис.14.5) имеет толщину 2а, высоту h (h >> 2а) и большую протяженность в направлении, перпендикулярном рисунку. Средняя плотность магнитного потока по сечению листа
. Лист (рис.14.5) имеет толщину 2а, высоту h (h >> 2а) и большую протяженность в направлении, перпендикулярном рисунку. Средняя плотность магнитного потока по сечению листа 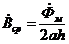 .
.
 |
Задача состоит в определении законов изменения
 и
и  по сечению листа. В силу симметрии напряженность магнитного поля на левой поверхности листа та же, что и на правой поверхности листа. Обозначим ее через
по сечению листа. В силу симметрии напряженность магнитного поля на левой поверхности листа та же, что и на правой поверхности листа. Обозначим ее через  и будем полагать известной (в дальнейшем выразим ее через
и будем полагать известной (в дальнейшем выразим ее через  ).
).
Рис. 14.5. Магнитный поверхностный эффект в стальном листе.
Так как толщина листа 2а много меньше высоты листа h, то искажающим влиянием краев листа на поле можно в первом приближении пренебречь и считать, что в лист с двух сторон проникает плоская электромагнитная волна. Расположим оси координат декартовой системы в соответствии с рис. 14.5. Примем, как и прежде,  . Общее решение для
. Общее решение для  таково:
таково:  , где р =
, где р =  - постоянная распространения волны. Из граничных условий найдем постоянные интегрирования. При z = -а, т. е. для точек, находящихся на левой стороне листа,
- постоянная распространения волны. Из граничных условий найдем постоянные интегрирования. При z = -а, т. е. для точек, находящихся на левой стороне листа,
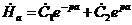 ; (14.20)
; (14.20)
при z =+а
 . (14.21)
. (14.21)
Совместное решение (14.20) и (14.21) относительно C1 и C2 дает
 .
.
Следовательно, в произвольной точке
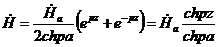 . (14.22)
. (14.22)
Напряженность электрического поля
 ,
,
где
 . (14.23)
. (14.23)
При z = + а напряженность  направлена вверх (вдоль оси — х); при z = — а — вниз (вдоль оси + х, см. рис.14.5, а). Вектор Пойнтинга направлен к средней плоскости листа (внутрь листа).
направлена вверх (вдоль оси — х); при z = — а — вниз (вдоль оси + х, см. рис.14.5, а). Вектор Пойнтинга направлен к средней плоскости листа (внутрь листа).
Как известно из раздела I учебника, ток, возникающий при прохождении по листу переменного магнитного потока, принято называть вихревым. Вектор плотности вихревого тока  = g
= g  в любой точке листа коллинеарен с вектором
в любой точке листа коллинеарен с вектором  в этой же точке. Магнитная индукция в произвольной точке
в этой же точке. Магнитная индукция в произвольной точке
 . (14.24)
. (14.24)
Среднее значение магнитной индукции в листе
 . (14.25)
. (14.25)
Если считать Вер известной и равной,  то из (14.25) можно найти напряженность поля на поверхности листа:
то из (14.25) можно найти напряженность поля на поверхности листа:
 . (14.26)
. (14.26)
Заметим, что аргумент ра = ka + jka является комплексом и th pa есть гиперболический тангенс от комплексного аргумента; он также является комплексом:
th ра = th (ka + jka) =  . (14.27)
. (14.27)
Отношение среднего значения магнитной индукции по сечению листа  к напряженности поля на поверхности листа
к напряженности поля на поверхности листа  называют комплексной магнитной проницаемостью:
называют комплексной магнитной проницаемостью:
 .
.
Она зависит от величины m, частоты w и толщины листа. При больших значениях аргумента 2ka sh 2ka» ch 2ka, значения этих функций намного больше 1. Поэтому при больших значениях 2ka

и комплексная магнитная проницаемость  .
.
Так, например, при толщине листа 2 а = 0,015 см, m = 20000,
g = 1,8*106 (Ом*м)-1 и
f = 50000 Гц;  = 84200; p =
= 84200; p =  ;
;
ka = 6,31; 2 ka = 12,62; th pa =  1. Следовательно,
1. Следовательно,
 .
.
Напряженность поля в средней плоскости листа (при z = 0)  . Отношение напряженности поля на краю листа (при z = a) к напряженности поля в средней плоскости листа:
. Отношение напряженности поля на краю листа (при z = a) к напряженности поля в средней плоскости листа:
 . (14.28)
. (14.28)
Левая и правая части формулы (14.28) являются комплексами. Модуль ch ра показывает, во сколько раз модуль Ha больше модуля H z=0.
Найдем модуль ch ра. С этой целью запишем два сопряженных комплекса:
ch (ka + jka) = ch ka cos ka + jsin ka sin ka
и
ch (ka — jka) = ch ka cos ka — j sh ka sin ka.
Произведение сопряженных комплексов дает квадрат модуля. Следовательно,
|ch pa |2 = ch (ka + jka) ch (ka — jka) = 1/2[ch 2ka + cos 2ka ].
Таким образом,
 . (14.29)
. (14.29)
Рассмотрим числовой пример. Пусть m = 100; f = 500 Гц;
g = 107 (Ом·м)-1. При этом k = 1410 м-1. Найдем отношение напряженности поля в средней плоскости к напряженности поля на поверхности листа при толщине листа: 2 а = 1 мм; 2 мм; 4 мм;2 ka = l,41; 2,82; 5,64;
 = 0,91; 0,52; 0,1.
= 0,91; 0,52; 0,1.
Таким образом, напряженность поля в средней плоскости листа может быть много меньше напряженности поля на краю листа.
Явление неравномерного распределения поля по сечению проводящего тела, вызванное затуханием электромагнитной волны при ее распространении в проводящую среду, называют поверхностным эффектом. Если вдоль листа направлен магнитный поток, то поверхностный эффект часто называют магнитным, если вдоль плоской шины направлен переменный ток, то поверхностный эффект часто называют электрическим поверхностным эффектом. Природа их одна и та же, а слова «магнитный» или «электрический» свидетельствуют лишь о том, что направлено вдоль листа (шины): поток или ток.
На рис. 14.5 б построены две кривые. Кривая Н (z) характеризует изменение модуля напряженности магнитного поля в функции от z. В средней плоскости листа Н до нуля не снижается, так как ch ¹ 0. Кривая Н строится по уравнению (14.22). Кривая Е(z) характеризует изменение модуля напряженности электрического поля в функции от z. Эта кривая строится по (14.23); sh pz z=0 = 0 и потому кривая проходит через нуль при z = 0. Кривая плотности вихревых токов d = g E качественно повторяет кривую Е от z (разница только в масштабе).
 |
Электрический поверхностный эффект в плоской шине. Эффект близости. При электрическом поверхностном эффекте -(рис.14.6, а) - вдоль пластины (шины) направлен синусоидальный ток I частоты w.
Рис. 14.6. Электрический поверхностный эффект в плоской шине.
В этом случае поле внутри пластины определяется по формулам:
 ,
,  ,
,  .
.
Сопротивление единицы длины шины (пластины)
Z = R + jX = 
Зависимость модуля Н(z) в этом случае такая же, как и зависимость Е(z) на рис. 14.5, б, а зависимость Е(z) такая же, как и зависимость Н(z) на этом же рисунке.
Если по двум параллельным близко расположенным плоским шинам (рис. 14.6, б) будет протекать в противоположных направлениях синусоидально изменяющийся во времени ток I частоты w, а размеры 2а << h и 2b << h, то, поместив начало декартовой системы координат в средней плоскости левой шины и учтя, что слева от левой шины напряженность поля Н = 0, а в пространстве между шинами H = - I/h (в этом можно убедиться на основании закона полного тока), получим формулы для H и E в левой шине:
 ,
,  .
.
Эпюра модулей Н и Е в функции от координаты z показана на рис 14.6, б. Поле одной шины влияет на распределение поля в другой шине. Это явление называют эффектом близости. Комплексное сопротивление единицы длины двух плоских шин, расположенных в воздухе равно двум комплексным сопротивлениям самих шин плюс индуктивное сопротивление, обусловленное магнитным потоком, проходящим в пространстве между шинами,
Z = R + jX =  .
.
Распространение электромагнитных волн в однородном и изотропном диэлектрике. Проводимость у идеального диэлектрика равна нулю. Поэтому в первом уравнении Максвелла (14.1) первое слагаемое правой части (d = gЕ) выпадает, и уравнения Максвелла для диэлектрика получают следующий вид:
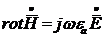 ; (14.30)
; (14.30)
 . (14.31)
. (14.31)
div  и
и  .
.
Для однородных и изотропных диэлектриков ma = const и условие div ma  = 0 равносильно условию div
= 0 равносильно условию div  = 0. Решим совместно уравнения (14.30) и (14.31). С этой целью возьмем ротор от уравнения (14.30). Получим rot rot
= 0. Решим совместно уравнения (14.30) и (14.31). С этой целью возьмем ротор от уравнения (14.30). Получим rot rot  = grad div
= grad div  — Ñ2
— Ñ2  = jwea rot
= jwea rot  . Так как div
. Так как div  = 0, то и grad div
= 0, то и grad div  = 0. В свою очередь rot
= 0. В свою очередь rot  на основании второго уравнения Максвелла равен —jwma
на основании второго уравнения Максвелла равен —jwma  . Поэтому
. Поэтому

или
 . (14.32)
. (14.32)
Произведение eama измеряется в с2 /м2:
[ea][ma] =  =c2/м2.
=c2/м2.
т. е. eama имеет размерность, обратную размерности квадрата скорости, и потому можно принять eama = 1/u2. После введения такого обозначения уравнение (14.32) получает следующий вид:
 . (14.32/)
. (14.32/)
Для плоской электромагнитной волны, распространяющейся в направлении оси z в соответствии с предыдущим, можно принять, что напряженность магнитного поля направлена вдоль оси y, т. е.
 . (14.33)
. (14.33)
Так как для плоской волны  зависит только от координаты z и не зависит от координат х и у, то уравнение
зависит только от координаты z и не зависит от координат х и у, то уравнение

приобретает следующий вид:
 (14.34)
(14.34)
Уравнению (14.34) соответствует характеристическое уравнение  корни которого
корни которого  и
и  . Общее решение уравнения (14.33):
. Общее решение уравнения (14.33):
 , (14.35)
, (14.35)
где С1 и С2 — комплексные коэффициенты, зависящие от граничных условий. Как и всякое комплексное число, их можно представить в показательной форме:  и
и  . Слагаемое
. Слагаемое  представляет собой падающую волну, продвигающуюся в положительном направлении оси z, а слагаемое
представляет собой падающую волну, продвигающуюся в положительном направлении оси z, а слагаемое 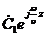 — отраженную волну, распространяющуюся в отрицательном направлении оси z.
— отраженную волну, распространяющуюся в отрицательном направлении оси z.
Напряженность электрического поля  найдем по уравнению (14.30):
найдем по уравнению (14.30):
 .
.
Как следует из предыдущего, для плоской волны
 .
.
Поэтому
 .
.
Величину  называют волновым сопротивлением диэлектрика:
называют волновым сопротивлением диэлектрика:  . Волновое сопротивление является чисто действительным числом (измеряется в омах):
. Волновое сопротивление является чисто действительным числом (измеряется в омах):
 Ом
Ом
Оно не зависит от угловой частоты колебаний w. Для вакуума e = 1 и m = 1, поэтому Zв = 377 Ом. Следовательно,
 , (14.36)
, (14.36)
где
 .
.
Присутствие единичного орта оси х (орта i) в формуле (14.36) свидетельствует о том, что вектор напряженности электрического поля направлен по оси х.
Таким образом, в плоской электромагнитной волне, распространяющейся в диэлектрике, как и для проводящей среды, Е и H взаимно перпендикулярны: Н направлено по оси у, E - по оси х.
Запишем выражения для мгновенных значений E и H падающей волны. Чтобы получить мгновенное значение падающей волны Н, необходимо комплекс  умножить на еjwt и от произведения взять мнимую часть. В результате получим
умножить на еjwt и от произведения взять мнимую часть. В результате получим
 |
 ; (14.37)
; (14.37) аналогично,
 . (14.38)
. (14.38)
По мере продвижения падающей волны вдоль оси z амплитуды E и Н остаются неизменными, т. е. затухания волны не происходит, так как в диэлектрике нет токов проводимости и выделения энергии в виде теплоты. На рис. 14.7 изображены пространственные кривые, представляющие собой графики мгновенных значений Н и Е. Эти графики построены по уравнениям (14.37) и (14.38) для момента времени wt+yn=0.
Рис.14.7. Графики мгновенных значений Е и Н
для момента времени wt + yn = 0.
Для более позднего момента времени, например для wt + yn = 90°, аналогичные кривые изображены на рис. 14.8.
Как видно из рис. 14.7 и 14.8, вектор Е при его изменении остается направленным в плоской волне вдоль оси х, а вектор Н — вдоль оси у, сдвига по фазе между Н и Е нет.
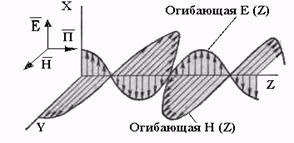 |
Рис. 14.8. Графики мгновенных значений Е и Н
для момента времени wt + yn = 900.
Проверим правильность построения графика Е = f (z) на рис. 14.7. Кривые на рис.14.7 построены при wt + yn = 0, поэтому уравнением кривой Е = f (z) является выражение [в соответствии с (14.38)]:
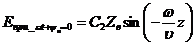 .
.
При z = 0 Е = 0. В интервале от  =0 до
=0 до  =p мгновенное значение Е отрицательно. При
=p мгновенное значение Е отрицательно. При  =p E = 0 и т. д. Вектор Пойнтинга падающей волны направлен вдоль оси z. Модуль П изменяется по закону
=p E = 0 и т. д. Вектор Пойнтинга падающей волны направлен вдоль оси z. Модуль П изменяется по закону
 .
.
Так как  , то
, то
 ,т. е. вектор Пойнтинга имеет постоянную составляющую
,т. е. вектор Пойнтинга имеет постоянную составляющую  и переменную, изменяющуюся во времени с двойной угловой частотой.
и переменную, изменяющуюся во времени с двойной угловой частотой.
Фазовая скорость электромагнитной волны в диэлектрике:
 . (14.39)
. (14.39)
Если волна распространяется в вакууме, то eа = e0 и mа = m0, и тогда фазовая скорость равна скорости света:
 300 000 км/с.
300 000 км/с.
Таким образом, фазовая скорость электромагнитной волны в диэлектрике очень велика, и она несоизмеримо больше фазовой скорости плоской электромагнитной волны в проводящей среде.
Длина волны l есть расстояние вдоль оси z, на котором фаза колебания изменится на 2p. Ее находят из соотношения  .
.
Отсюда
 . (14.40)
. (14.40)
Из (14.40) видно, что длина волны в диэлектрике обратно пропорциональна частоте f. Так, при f = 106 Гц l = = 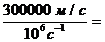 300 м.
300 м.
 2017-12-14
2017-12-14 1850
1850
