Выражение вектора через проекции (декартовы прямоугольные координаты):
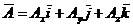 ;
;  ;
;
cos  ; cos
; cos 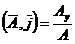 ; cos
; cos  .
.
Сумма двух векторов: 
 ;
;
Sx = Ax + Bx; Sy = Ay + By; Sz = Az + Bz;
Разность двух векторов: 
 ;
;
Rx = Ax - Bx; Ry = Ay - By; Rz = Az - Bz;
Скалярное произведение двух векторов:
А*В = АВ cos (А, В) = AxBx + АyВy + АzВz.
Векторное произведение двух векторов:
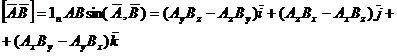 ,
,
где 1n—единичный вектор по нормали к плоскости, в которой лежат перемножаемые векторы А и В.
Уравнение линии вектора А:  ;
;  .
.
Дифференциальный оператор Гамильтона — набла.
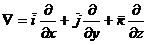 .
.
Сам вектор Ñ не имеет реального значения, он приобретает определенный смысл лишь в комбинации со скалярными или векторными функциями.
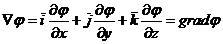 .
.
Скалярное произведение Ñ на вектор E:
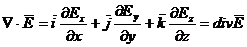 .
.
 .
.
Градиент потенциала: 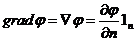 ,
,
где 1n—единичный вектор по нормали к поверхности j = const.
Свойства вихря вектора: divrot a = 0 rot(a + b) = rot a + rot b,
rot(U a) = Urot a + gradU´ a, div a ´ b = b rot a – a rot b.
Поток вектора через поверхность S:  .
.
Дивергенция вектора:  .
.
Теорема Гаусса:  .
.
Циркуляция вектора:  .
.
Ротор вектора:  .
.
Проекция ротора на направление n:
 ,
,
где площадка DS нормальна к направлению n.
Теорема Стокса:  ,
,
где L—периметр поверхности S.
Лапласиан скаляра j:  .
.
Лапласиан вектора А:  .
.
Ротор градиента:  .
.
Дивергенция ротора:  .
.
Дивергенция произведения скаляра и вектора:
 .
.
Дивергенция векторного произведения: div[ EH ] = H rot E - E rot H.
Ротор от ротора: rot rot A = grad div A - Ñ2 A.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Запишите уравнения Максвелла для случая когда векторы Н и Е являются синусоидальными функциями времени.
2. Кто впервые доказал, что электромагнитная волна переносит энергию и импульс?
3. Чему равна разность потоков вектора Пойнтинга через поперечное сечение кабеля в его начале и в его конце?
4. Почему в уравнениях электромагнитного поля нельзя использовать скалярный потенциал электростатического поля? Как определяется скалярный потенциал электромагнитного поля?
5. Укажите особенности электромагнитного поля в ближней и дальней зоне электрического вибратора.
 2017-12-14
2017-12-14 1306
1306







