Одной из важных задач при построении помехоустойчивых кодов с заданными характеристиками, является установление соотношений между его способностью обнаруживать или исправлять ошибки и избыточностью.
Существуют граничные оценки, связывающие 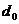 ,
,  и
и 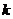 или
или 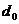 и
и  .
.
Граница Хэмминга для высокоскоростных кодов определяется соотношениями:
Для кода с основанием  :
:
 , где
, где 
Для двоичного кода:

Граница Плоткина для низкоскоростных кодов определяется соотношением:
Для кода с основанием  :
:

Для двоичного кода:

Границы Хэмминга и Плоткина являются верхними границами для кодового расстояния при заданных  и
и 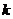 . Верхняя граница – число, близкое к истинному значению кодового расстояния и заведомо больше его. Они определяют минимальное число проверочных разрядов
. Верхняя граница – число, близкое к истинному значению кодового расстояния и заведомо больше его. Они определяют минимальное число проверочных разрядов  , при котором существует помехоустойчивый код, имеющий кодовое расстояние
, при котором существует помехоустойчивый код, имеющий кодовое расстояние 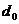 и гарантированно исправляющий ошибки кратностью
и гарантированно исправляющий ошибки кратностью 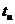 .
.
Для высокоскоростных кодов с  , при выполнении условия, заданного границей Хэмминга, автоматически вытекает выполнение условия, заданного границей Плоткина. Для низкоскоростных кодов (< 0,4) более сильной является граница Плоткина.
, при выполнении условия, заданного границей Хэмминга, автоматически вытекает выполнение условия, заданного границей Плоткина. Для низкоскоростных кодов (< 0,4) более сильной является граница Плоткина.
При проектировании кода, необходимо выполнение и условия Хэмминга и условия Плоткина, поэтому граница Плоткина используется при разработке низкоскоростных кодов, а граница Хэмминга – при проектировании высокоскоростных кодов.
Граница Варшамова–Гильберта (нижняя граница) определяется соотношением:
Для кода с основанием  :
:

Для двоичного кода:

Она показывает, при каком значении  существует код, гарантированно имеющий кодовое расстояние
существует код, гарантированно имеющий кодовое расстояние 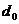 .
.
Рассмотрим примеры использования этих границ.
Пример 1.
Предположим, что нужно найти код, длиной  = 63 с
= 63 с 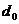 = 5 и наибольшее возможное значение
= 5 и наибольшее возможное значение 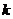 . Существует код Боуза–Чоудхури–Хоквингема (БЧХ) с
. Существует код Боуза–Чоудхури–Хоквингема (БЧХ) с 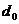 = 5,
= 5,  = 63 и
= 63 и 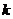 = 51. Для оценки, насколько хорошим является этот код, используются границы Хэмминга и Варшмова–Гильберта. Граница Хэмминга дает:
= 51. Для оценки, насколько хорошим является этот код, используются границы Хэмминга и Варшмова–Гильберта. Граница Хэмминга дает:



Граница Варшамова–Гильберта дает:



Таким образом, из границы Хэмминга следует, что не существует кодов с  , меньше 11, а граница Варшамова–Гильберта гарантирует существование таких кодов с
, меньше 11, а граница Варшамова–Гильберта гарантирует существование таких кодов с  . Следовательно, код с
. Следовательно, код с  = 63 и
= 63 и 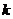 = 51 является хорошим и дальнейшие поиски могут привести к незначительным улучшениям.
= 51 является хорошим и дальнейшие поиски могут привести к незначительным улучшениям.
Пример 2.
Предположим, что нужно построить код, способный исправлять ошибки, кратности 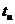 = 2 и имеющий 2 информационных разряда (
= 2 и имеющий 2 информационных разряда (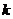 = 2).
= 2).
В соответствии с пунктом 2.1.2:  . Определим минимальное значение
. Определим минимальное значение  , необходимое в данном коде. В соответствии с границей Хэмминга, имеем:
, необходимое в данном коде. В соответствии с границей Хэмминга, имеем:

Данному неравенству удовлетворяет значение  = 7. Однако, если воспользоваться границей Плоткина:
= 7. Однако, если воспользоваться границей Плоткина:
 , следовательно, минимальное целое
, следовательно, минимальное целое  = 8.
= 8.
Из границы Хэмминга следует, что не может быть искомого кода с  , а из границы Плоткина – с
, а из границы Плоткина – с  , поэтому
, поэтому  .
.
 2017-12-16
2017-12-16 1265
1265
