Тема 6. Границі функції

Границя функції

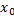Говорять, що число A є границею функції при, x що прямує до , якщо для будь-якої послідовності значень аргументу (1), яка збігається до числа, 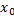послідовність значень функції (2) збігається до числа A, і пишуть

, або ∱(x)

Нескінченно малі величини

Послідовність 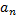називається нескінченно малою, якщо .=0 Наприклад, послідовність чисел - Нескінченно мала.

Функція називається нескінченно малою в околиці точки 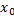, Якщо. =0

Функція називається нескінченно малою на нескінченності, якщо 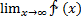=0 або.

Також нескінченно малою є функція, що є різниця функції та її межі, тобто якщо, = то ∱(x) =

Нескінченно великі величини.

У всіх наведених нижче формулах нескінченність праворуч від рівності мається на увазі певного знаку (або "плюс", або "мінус"). Тобто, наприклад, функція x sin x, Необмежена з обох сторін, не є нескінченно великою при

Послідовність 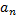називається нескінченно великою, якщо. =∾

Функція називається нескінченно великою в околиці точки 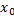, Якщо

Функція називається нескінченно великою на нескінченності, якщо 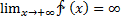або або

4,Основні формули про границі.