 3.2.1. Понятие производной. Производные основных элементарных функций
3.2.1. Понятие производной. Производные основных элементарных функций
Изучая поведение функции у=f (x) около конкретной точки x 0 (рис. 3.16), важно знать, как меняется значение функции при изменении значения аргумента. Для этого используются понятия приращений аргумента и функции.
Пусть функция f (x) определена в некоторой окрестности точки x 0 и пусть х 1 – произвольная точка этой окрестности.
Определение 3.2.1. Приращением аргумента при переходе от точки x 0 к точке x 1называют число Dх = х 1– x 0, а разность D у=f (x 1) –f (x 0) называют приращением функции при этом переходе.
Для приращения функции также применяют обозначение D f.
Поскольку х 1– x 0= Dх, то х 1= x 0+ Dх. Тогда
D у=f (x 0+ Dх) –f (x 0).
Определение 3.2.2. Если существует предел отношения 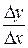 приращения функции Δ у к вызвавшему его приращению аргумента Δ х, когда Δ х стремится к нулю, то этот предел называется производной функции у = f (х) в данной точке x 0и обозначается через
приращения функции Δ у к вызвавшему его приращению аргумента Δ х, когда Δ х стремится к нулю, то этот предел называется производной функции у = f (х) в данной точке x 0и обозначается через 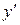 :
:
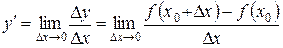 .
.
Подчеркнем, что производная 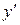 функции y – это новая функция, определенная во всех точках х, в которых существует
функции y – это новая функция, определенная во всех точках х, в которых существует 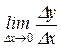 .
.
Производную функции также обозначают 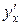 или
или 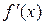 .
.
Для нахождения производной функции y=f (x) по определению 3.2.2. необходимо:
-придать аргументу х приращение 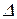 х;
х;
-найти значение функции в точке x 0 + 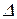 x, т.е. найти f (x 0 +
x, т.е. найти f (x 0 + 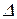 x);
x);
-найти приращение функции: D у=f (x 0+ Dх) –f (x 0);
-составить отношение 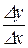 ;
;
-вычислить предел 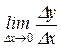 .
.
Пример 3.2.1. Найти производную 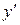 функции y=f (x) =x2.
функции y=f (x) =x2.
○Рассмотрим приращение 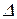 х аргумента в точке х: Dх = х 1– х.
х аргумента в точке х: Dх = х 1– х.
Тогда f (x+ 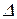 x) = (x+
x) = (x+ 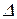 x) 2=x2+2x
x) 2=x2+2x 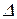 x+ (
x+ (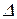 x) 2.
x) 2.
Приращение функции
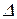 y=f (x+
y=f (x+ 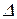 x)– f (x) =x2+2x
x)– f (x) =x2+2x 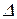 x+ (
x+ (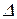 x) 2 – x2 = 2x
x) 2 – x2 = 2x 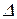 x+ (
x+ (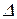 x) 2.
x) 2.
Отсюда 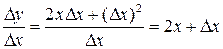 и
и
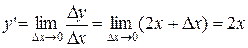 .●
.●
Отметим, что если существует предел справа 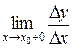 (или предел слева
(или предел слева 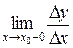 ), то он называется правой (или левой) производной функции f (х) в точке х 0.
), то он называется правой (или левой) производной функции f (х) в точке х 0.
Действие нахождения производной функции называется ее дифференцированием, а функция, имеющая производную в точке х, называется дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой на этом промежутке. При этом, если промежуток от а до b есть отрезок [ a; b ], то в точке а речь идет о правой производной, а в точке b – о левой производной.
Приведем таблицу производных основных элементарных функций:
| у=С | 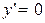 , С - постоянная (число) , С - постоянная (число)
| |
| у=xa | 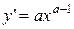 , a , a 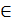 R, х >0 R, х >0
| |
| Отсюда: | ||
| у=x | 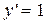
| |
y= 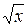
| 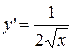
| |
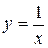
| 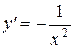
| |
| у= sin x | 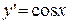
| |
| у= cos x | 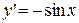
| |
| у=tg x | 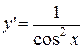 , , 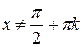 , k , k 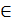 Z Z
| |
| у=ctg x | 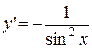 , , 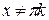 , k , k 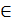 Z Z
| |
| у=ax | 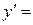 ax ln a, а >0 ax ln a, а >0
| |
| у=ex | 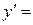 ex ex
| |
| у= log ax | 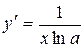 , a >0, a ¹1, x >0 , a >0, a ¹1, x >0
| |
| у= ln x | 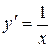 , x >0 , x >0
| |
| у= arcsin x | 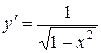 , x , x 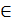 (–1, 1) (–1, 1)
| |
| y= arccos x | 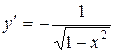 , x , x 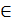 (–1, 1) (–1, 1)
| |
| у= arctg x | 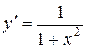
| |
| у= arcctg x | 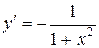
|
 2017-10-31
2017-10-31 338
338







