Пусть  , а
, а  – любые две дифференцируемые функции своих аргументов. Тогда функция
– любые две дифференцируемые функции своих аргументов. Тогда функция  – так называемая сложная функция от x (она представляет собой функцию от функции). Найдем ее производную
– так называемая сложная функция от x (она представляет собой функцию от функции). Найдем ее производную  (производную от y по x). Для этого дадим аргументу x некоторое приращение
(производную от y по x). Для этого дадим аргументу x некоторое приращение  , то есть перейдем от x к
, то есть перейдем от x к  . Приращение
. Приращение  величины x вызовет некоторое приращение
величины x вызовет некоторое приращение 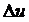 величины u, а то, в свою очередь, вызовет некоторое приращение
величины u, а то, в свою очередь, вызовет некоторое приращение 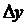 величины y. Так как функции
величины y. Так как функции  и
и  являются, по условию, дифференцируемыми функциями своих аргументов, то они являются и непрерывными функциями своих аргументов. То есть при
являются, по условию, дифференцируемыми функциями своих аргументов, то они являются и непрерывными функциями своих аргументов. То есть при  и
и  , и
, и 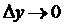 . А тогда, согласно определению производной, получаем:
. А тогда, согласно определению производной, получаем:
 .
.
Итак, если  – сложная функция от x, то
– сложная функция от x, то  . Или, опуская значок x (но подразумевая его) запишем короче:
. Или, опуская значок x (но подразумевая его) запишем короче:
 (1)
(1)
Формула (1) представляет собой правило вычисления производной (правило дифференцирования) сложной функции.
Собственно говоря, суть правила (1) проста. А именно, если функция  – простая функция от x (из числа основных элементарных функций, чьи производные содержатся в таблице производных), то ее производная и выглядит, и находится просто:
– простая функция от x (из числа основных элементарных функций, чьи производные содержатся в таблице производных), то ее производная и выглядит, и находится просто:  . А если
. А если  , где
, где  – две простых функции, то
– две простых функции, то  – уже сложная функция от x. Ее производная
– уже сложная функция от x. Ее производная  по x находится уже по формуле (1): сначала находим производную от функции
по x находится уже по формуле (1): сначала находим производную от функции  по переменной u (точно так же, как находим производную от функции
по переменной u (точно так же, как находим производную от функции  по переменной x), а затем умножаем ее на производную функции
по переменной x), а затем умножаем ее на производную функции  по переменной x.
по переменной x.
Чтобы сделать наглядным применение этого правила, приведем таблицу сравнения, содержащую производные некоторых простых и аналогичных им сложных функций от x:
Таблица 1.
| Производные простых функций (x – независимая переменная) | Производные сложных функций ( – любая дифференцируемая функция) – любая дифференцируемая функция) | |
1.  | 1.  | |
2. 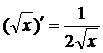 | 2.  | |
3.  | 3. 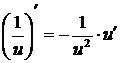 | |
4.  | 4.  | |
5.  | 5.  | |
6.  | 6.  | |
| (……) | (……) |
Таблица (1) наглядно иллюстрирует разницу между производными простых и сложных функций.
Пример 1.  ;
; 
Решение.
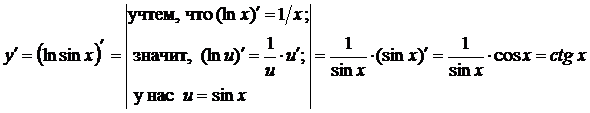
Пример 2. 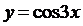 ;
; 
Решение.
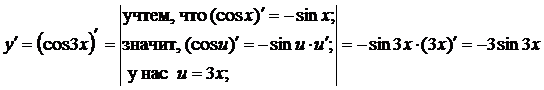
Пример 3.  ;
; 
Решение.

Пример 4.  ;
; 
Решение.
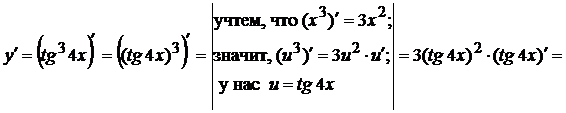
 .
.
Пусть теперь  и
и  – любые две дифференцируемые функции. Тогда
– любые две дифференцируемые функции. Тогда  – сложная функция от x. И ее дифференциал dy, как оказывается, можно найти по любой из двух следующих формул:
– сложная функция от x. И ее дифференциал dy, как оказывается, можно найти по любой из двух следующих формул:
1) 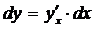 ; 2)
; 2) 
Данные формулы выражают так называемое свойство инвариантности формы дифференциала функции. Согласно этого свойства, дифференциал функции имеет форму произведения производной этой функции на дифференциал ее аргумента независимо от того, является ли ее аргумент независимой переменной (x) или функцией (u) от другого аргумента.
Действительно, если x – независимая переменная, то дифференциал dy функции y, зависящей от x, находится, по первой из этих формул. Но так как  – сложная функция от x, то используя формулу (1) для производной сложной функции, получим:
– сложная функция от x, то используя формулу (1) для производной сложной функции, получим:
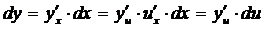
То есть приходим ко второй формуле.
Производная функции, заданной неявно.
Если функция  задана в неявном виде, то есть задана уравнением
задана в неявном виде, то есть задана уравнением 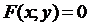 (в этом уравнении y не выражен через x, и выразить его не удается), то при нахождении производной
(в этом уравнении y не выражен через x, и выразить его не удается), то при нахождении производной  такой функции поступают следующим образом:
такой функции поступают следующим образом:
1) Дифференцируют обе части уравнения 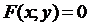 по x, помня при этом, что y – это функция от x. В результате появляется некоторое равенство
по x, помня при этом, что y – это функция от x. В результате появляется некоторое равенство  , содержащее искомую производную
, содержащее искомую производную  .
.
2) Выражают из полученного равенства эту производную.
Таким образом, производную  функции y, заданной неявно уравнением
функции y, заданной неявно уравнением 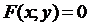 , находят по схеме:
, находят по схеме:
 (2)
(2)
Пример 5. Найти производную  функции y, заданной неявно уравнением
функции y, заданной неявно уравнением 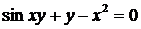 .
.
Решение.
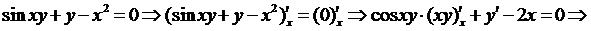


Производная функции, заданной параметрически.
Если функция задана в параметрической форме
 , (3)
, (3)
то ее производную  находят по формуле:
находят по формуле:
 . (4)
. (4)
Подтвердим эту формулу. Пусть  и
и  – дифференцируемые функции параметра t. Зафиксируем некоторое t, а затем придадим ему приращение
– дифференцируемые функции параметра t. Зафиксируем некоторое t, а затем придадим ему приращение 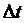 . При этом x и y получат некоторые приращения
. При этом x и y получат некоторые приращения  и
и  , причем при
, причем при 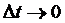 и
и 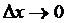 , и
, и  (функции
(функции  и
и  – дифференцируемые, а значит, и непрерывные). А тогда
– дифференцируемые, а значит, и непрерывные). А тогда
 .
.
Пример 6. Функция  , заданная параметрически уравнениями
, заданная параметрически уравнениями

 ,
,
представляет собой параметрическое уравнение окружности с центром в начале координат и радиусом R (рис. 1).
Найдем производную  этой функции:
этой функции:

Упражнения
1. Найти угол наклона к оси ох касательной, проведенной к параболе  в точке
в точке 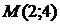 .
.
Ответ:  .
.
2. Найти на параболе  такую точку
такую точку  , чтобы касательная к параболе, проведенная в этой точке, составила с осью ох угол
, чтобы касательная к параболе, проведенная в этой точке, составила с осью ох угол 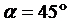 .
.
Ответ:  .
.
3. В момент времени 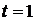 найти скорость v и ускорение a точки, движущейся по оси ох по закону
найти скорость v и ускорение a точки, движущейся по оси ох по закону  .
.
Ответ:  ;
;  .
.
4. Количество y произведенной за время t продукции описывается функцией  . Найти производительность труда предприятия.
. Найти производительность труда предприятия.
Ответ: 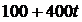 (ед. продукции за ед. времени).
(ед. продукции за ед. времени).
5. Функция  определяет зависимость себестоимости продукции y (в рублях) от объема x выпускаемой продукции (в некоторых единицах). Найти предельную себестоимость продукции.
определяет зависимость себестоимости продукции y (в рублях) от объема x выпускаемой продукции (в некоторых единицах). Найти предельную себестоимость продукции.
Ответ:  (руб/ед.).
(руб/ед.).
6. Кривая спроса  имеет уравнение
имеет уравнение  . Найти предельный (маржинальный) доход от реализации продукции.
. Найти предельный (маржинальный) доход от реализации продукции.
Ответ:  (ден. ед./ед. товара).
(ден. ед./ед. товара).
7. Найти производную  функций:
функций:
а) 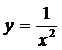 ; б)
; б)  ; в)
; в)  ; г)
; г) 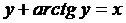 ; д)
; д) 
Ответ: а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 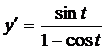 .
.
Производная обратной функции.
Пусть дана возрастающая или убывающая функция  , определенная на некотором отрезке
, определенная на некотором отрезке  . Пусть f(a)=c, f(b)=d. Для определенности будем далее рассматривать возрастающую функцию.
. Пусть f(a)=c, f(b)=d. Для определенности будем далее рассматривать возрастающую функцию.
Рассмотрим два различных значения x1 и x2, принадлежащих отрезку 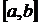 . Из определения возрастающей функции следует, что если x1 < x2 и
. Из определения возрастающей функции следует, что если x1 < x2 и  ,
,  , то y1<y2. Следовательно, двум различным значениям x1 и x2 соответствуют два различных значения функции y1 и y2. Справедливо и обратное, т.е. y1 < y2.
, то y1<y2. Следовательно, двум различным значениям x1 и x2 соответствуют два различных значения функции y1 и y2. Справедливо и обратное, т.е. y1 < y2.  , а
, а  , то из определения возрастающей функции следует, что x1 < x2. Таким образом, между значениями x и соответствующими значениями y устанавливается взаимно однозначное соответствие.
, то из определения возрастающей функции следует, что x1 < x2. Таким образом, между значениями x и соответствующими значениями y устанавливается взаимно однозначное соответствие.
Рассматривая эти значения y как значения аргумента, а значения x как значения функции, получаем x как функцию y:  .
.
Эта функция называется обратной для функции  . Очевидно, что 1) функция
. Очевидно, что 1) функция  является обратной для функции
является обратной для функции  ;
;
2) если возрастающая (или убывающая) функция  непрерывна на отрезке
непрерывна на отрезке 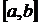 , причем f(a)=c, f(b)=d, то обратная функция определена и непрерывна на отрезке
, причем f(a)=c, f(b)=d, то обратная функция определена и непрерывна на отрезке  .
.
Теорема 1. Если для функции  существует обратная функция
существует обратная функция  , которая в рассматриваемой точке y имеет производную
, которая в рассматриваемой точке y имеет производную  , отличную от нуля, то в соответствующей точке x функция
, отличную от нуля, то в соответствующей точке x функция  имеет производную
имеет производную  , равную
, равную  , т.е. справедлива формула
, т.е. справедлива формула  .
.
Другими словами, производная одной из двух взаимно обратных функций равна единице, деленной на производную второй из этих функций при соответствующих значениях x и y.
Доказательство. Возьмем приращение  , тогда
, тогда 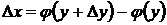 . Поскольку
. Поскольку  - монотонная функция, то
- монотонная функция, то  , а значит имеет место тождество
, а значит имеет место тождество  . (5)
. (5)
Так как функция  - непрерывная, то
- непрерывная, то  при
при  . Переходя к пределу при
. Переходя к пределу при  в обеих частях равенства (5), получим
в обеих частях равенства (5), получим
 или
или  ,
,
Что и требовалось получить.
Используя доказанную теорему, получим табличные производные функций y=arcsinx и y=arctgx.
Пример 7. Найти производную функции y=arcsinx.
Решение. Рассмотрим обратную функцию x=siny. Найдем  . На основании (5) имеем
. На основании (5) имеем 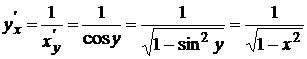 , т.е.
, т.е. 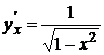 . Перед корнем берется знак плюс, так как функция y=arcsinx принимает значения на отрезке
. Перед корнем берется знак плюс, так как функция y=arcsinx принимает значения на отрезке 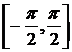 и, следовательно
и, следовательно  .
.
Пример 8. Найти производную функции y=arctgx.
Решение. Рассмотрим обратную функцию x=tgy. Найдем  . На основании (5) имеем
. На основании (5) имеем 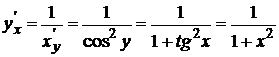 , т.е.
, т.е. 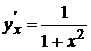 .
.
Логарифмическое дифференцирование или производная сложной показательной функции.
Сложной показательной функцией – называется функция у которой и основание и показатель степени являются функциями от х, например  ,
,  , вообще всякая функция вида
, вообще всякая функция вида 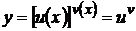 есть сложная показательная функция.
есть сложная показательная функция.
Теорема 1. Если 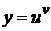 , то
, то 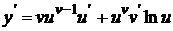 .
.
Доказательство. Логарифмируем функцию y:  . Дифференцируя полученное равенство по х, будем иметь:
. Дифференцируя полученное равенство по х, будем иметь: 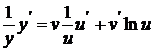 , откуда
, откуда  . Подставляя сюда выражение
. Подставляя сюда выражение 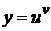 , получаем
, получаем 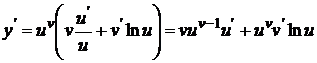 .
.
Таким образом, производная сложной показательной функции состоит из двух слагаемых: первое слагаемое получается, если при дифференцировании предположить, что и есть функция от х, а v есть постоянная (т.е. если рассматривать  как степенную функцию); второе слагаемое получается, если предположить, что v есть функция от х, а u=const (т.е. если рассматривать
как степенную функцию); второе слагаемое получается, если предположить, что v есть функция от х, а u=const (т.е. если рассматривать  как показательную функцию).
как показательную функцию).
Пример 9. Найти производную функции y=xх.
Решение. Логарифмируем функцию y: 
 . Дифференцируем полученное равенство по х:
. Дифференцируем полученное равенство по х:  . Таким образом,
. Таким образом,  . Учитывая условие задачи, получаем
. Учитывая условие задачи, получаем 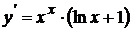 .
.
Пример 10. Найти производную функции y=  .
.
Решение. Логарифмируем функцию y: 
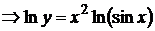 . Дифференцируем полученное равенство по х:
. Дифференцируем полученное равенство по х:  . Таким образом,
. Таким образом,  . Учитывая условие задачи, получаем
. Учитывая условие задачи, получаем 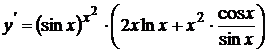 .
.
Упражнения
1) Найти производные функций, заданных неявно:
а) 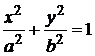 ; б)
; б)  ; в)
; в) 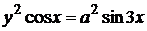 .
.
2) Найти производные функций, заданных параметрически:
а)  ; б)
; б)  ; в)
; в) 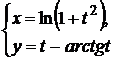
3) Найти производные сложных показательных функций.
а)  , б)
, б)  , в)
, в)  .
.
 2018-01-08
2018-01-08 6679
6679