Пусть вектор-функция 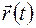 определена в окрестности точки
определена в окрестности точки 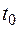 , кроме самой точки
, кроме самой точки 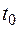 .
.
Вектор 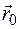 называется пределом векторной функции
называется пределом векторной функции 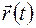 при
при 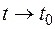 (или в точке
(или в точке 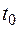 ), если
), если
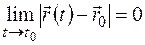 . (1.4)
. (1.4)
Если 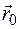 есть предел функции
есть предел функции 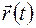 при
при 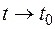 , то это записывается так
, то это записывается так
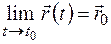 . (1.5)
. (1.5)
Если записать векторную функцию 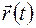 и вектор
и вектор 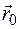 в проекциях
в проекциях
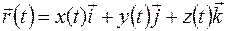 ,
,
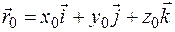 ,
,
то получим
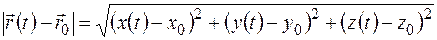 . (1.6)
. (1.6)
Тогда из равенства (1.4) следует, что
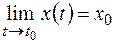 ,
, 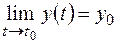 ,
, 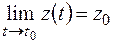 . (1.7)
. (1.7)
Свойства вектор-функции:
1. Если 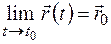 , то
, то 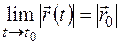 .
.
2. 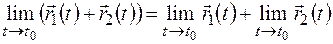 .
.
3. 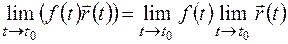 ,
, 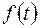 − скалярная функция.
− скалярная функция.
4. 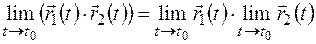
5. 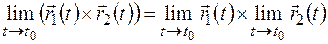 .
.
Вектор-функция 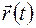 , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки 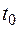 , называется непрерывной в точке
, называется непрерывной в точке 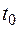 , если
, если 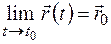 .
.
Из равносильности (1.4) и (1.7) следует, что для того чтобы вектор-функция 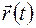 была непрерывной в точке
была непрерывной в точке 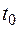 , необходимо и достаточно, чтобы в этой точке были непрерывны функции
, необходимо и достаточно, чтобы в этой точке были непрерывны функции 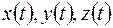 .
.
Введем понятие производной векторной функции
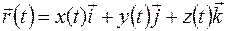 . (1.8)
. (1.8)
Предполагаем, что начало вектора 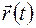 находится в начале системе координат (рис.1.2).
находится в начале системе координат (рис.1.2).
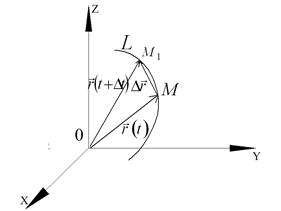
Рис. 1.2
Возьмем фиксированное значение параметра, соответствующее какой-либо точке определенной точке 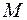 на кривой, заданной уравнением (1.8), и дадим параметру
на кривой, заданной уравнением (1.8), и дадим параметру 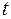 приращение
приращение 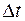 . Тогда получим вектор:
. Тогда получим вектор:
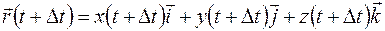 ,
,
который определяет некоторую точку 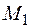 . Найдем приращение вектора:
. Найдем приращение вектора:
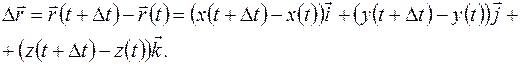 (1.9)
(1.9)
На рисунке, где 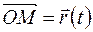 ,
, 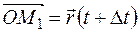 . Вектор приращения определяется вектором
. Вектор приращения определяется вектором 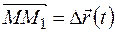 .
.
Рассмотрим отношение 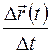 приращения вектор-функции к приращению скалярного аргумента; это есть вектор коллинеарный с вектором
приращения вектор-функции к приращению скалярного аргумента; это есть вектор коллинеарный с вектором 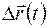 . При этом вектор
. При этом вектор 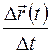 в сторону, соответствующую возрастанию параметра
в сторону, соответствующую возрастанию параметра 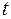 .
.
Далее с учетом (1.9) вектор 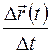 можно представить в виде
можно представить в виде
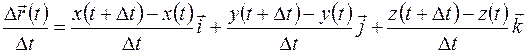 .(1.10)
.(1.10)
Если функции 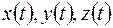 имеют производные при выбранном значении параметра
имеют производные при выбранном значении параметра 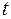 , то множители при
, то множители при 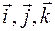 в равенстве (1.10) в пределе при
в равенстве (1.10) в пределе при 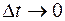 обратятся в производные
обратятся в производные 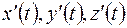 .
.
Значит, 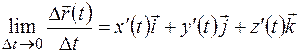 .
.
Вектор, определяемый последним равенством, называется производной от вектора 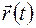 по скалярному аргументу
по скалярному аргументу 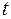 . Ее обозначают
. Ее обозначают 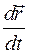 или
или 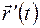 . Итак,
. Итак,
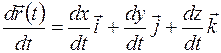 . (1.11)
. (1.11)
Выясним направление вектора 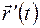 . Заметим, что при
. Заметим, что при 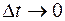 точка
точка 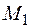 стремится к точке
стремится к точке 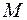 и поэтому секущая
и поэтому секущая 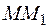 стремится к касательной в точке
стремится к касательной в точке 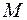 . Отсюда, производная
. Отсюда, производная 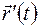 является вектором, касательным к годографу вектор-функции
является вектором, касательным к годографу вектор-функции 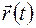 , направленным в сторону, соответствующую возрастанию параметра
, направленным в сторону, соответствующую возрастанию параметра 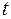 .
.
Из (1.11) следует, что
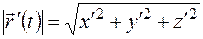 . (1.12)
. (1.12)
Дифференциал длины дуги кривой равен
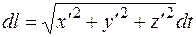 ,
,
откуда
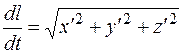 . (1.13)
. (1.13)
Из (1.12) и (1.13) имеем
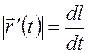 . (1.14)
. (1.14)
Таким образом, модуль производной вектор-функции 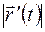 равен производной от длины годографа по аргументу
равен производной от длины годографа по аргументу 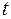 .
.
Правила дифференцирования вектор-функции:
1. Если 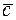 - постоянный вектор, то
- постоянный вектор, то 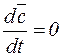 .
.
2. 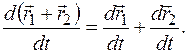
3. 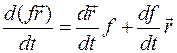 , где
, где 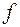 -скалярная функция.
-скалярная функция.
4. 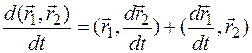 ,
, 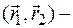 скалярное произведение.
скалярное произведение.
5. 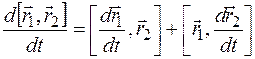 ,
, 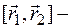 векторное произведение.
векторное произведение.
Последовательным дифференцированием можно найти производные высших порядков
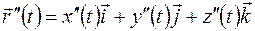 и т.д.
и т.д.
 2015-06-28
2015-06-28 1903
1903








