Точка  называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки
называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
, в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
Первое достаточное условие перегиба графика функции:
Пусть функция y = f(x) непрерывна в точке  , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки
, имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки  . Тогда, если в пределах этой окрестности слева и справа от
. Тогда, если в пределах этой окрестности слева и справа от  , вторая производная имеет разные знаки, то
, вторая производная имеет разные знаки, то  является точкой перегиба графика функции.
является точкой перегиба графика функции.
Второе достаточное условие перегиба графика функции:
Если  , а
, а  , тогда
, тогда  является абсциссой точки перегиба графика функции y= f(x).
является абсциссой точки перегиба графика функции y= f(x).
Третье достаточное условие перегиба графика функции.
Пусть  , а
, а 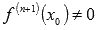 , тогда если n – четное число, то
, тогда если n – четное число, то  является абсциссой точки перегиба графика функции y = f(x).
является абсциссой точки перегиба графика функции y = f(x).
Асимптоты кривой.
Асимптота кривой с бесконечной ветвью — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.
Для гиперболы  асимптотами являются оси абсцисс и ординат. Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее
асимптотами являются оси абсцисс и ординат. Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее 
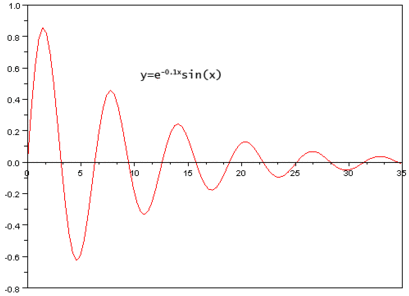
Затухающие колебания 
Кривая может бесконечное множество раз пересекать асимптоту


 2018-01-08
2018-01-08 717
717







